Professor Dr. Michael Dellnitz

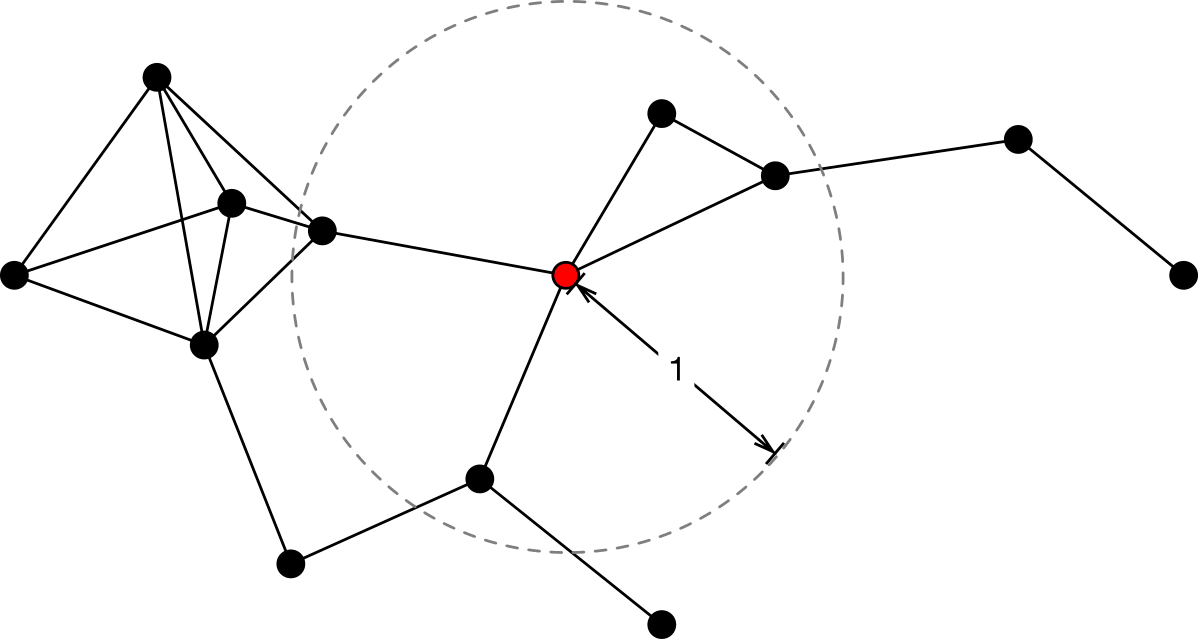
The goal of this project is to investigate the capabilities and limitations of local, distributed strategies for swarms of mobile robots. Such strategies consist of protocols run by the individual robots. They are supposed to guide the movements of the robots in such a way that globally a prescribed formation like gathering, forming a line or other shapes is reached from an arbitrary initial configuration of the robots. This research direction is well-established in distributed computing. Our approach is to combine techniques from distributed computing and dynamical systems research in order to enhance the understanding of protocols for such formation tasks. To this end, we analyze the speed of the protocols in terms of runtime complexity in the distributed computing sense as well as stability properties of the prescribed formation with the use of ideas from dynamical systems. While in the distributed computing community often only a worst-case analysis is considered, the tools of dynamical systems allow a more fine-grained analysis of the input configurations by exploring the state space. More concretely, the state space foliation describes the long-term dynamical behavior of input configurations in more detail, i.e. it allows to identify classes of configurations that converge comparably fast or slow and even classes that fail to converge to the prescribed formation. Thus, the combination of both views leads to a more profound understanding of distributed strategies for swarms of mobile robots.

Our research project: Multiobjective Optimization of Non-Smooth PDE-Constrained Problems - Switches, State Constraints and Model Order Reduction

Simultaneous Development and Testing of Cyber Physical Systems (CPS) using the example of autonomous electric vehicles (SET CPS)

dSPACE, e.GO Mobile, and the Institute of Industrial Mathematics Launch Research Project

Paderborn/Aachen, May 28, 2019. How can autonomous vehicles with electric drives be developed as examples of complex cyber-physical systems faster, more cost-effectively, and with lower resource consumption? And how can the safety of these vehicles on the road be increased? A team of researchers and developers from dSPACE, e.GO Mobile AG, and the Institute of Industrial Mathematics at the University of Paderborn started a research project a few weeks ago to answer this complex question. The project is funded by the German state of North Rhine-Westphalia (NRW) and the EU as part of the IKT.NRW lead market competition. The project, scheduled to run for 36 months, aims to simultaneously develop and test cyber-physical systems (CPS) using the example of an electric autonomous vehicle. It is abbreviated SET CPS according to its German title.

In vehicle development, trends such as automated driving and the development of alternative drives, such as battery-powered vehicles, are causing a sharp increase in the demands placed on the underlying systems. When these types of vehicles are developed, the aim is to optimize a large number of target parameters such as fuel consumption, range, and driving comfort, and to guarantee the safety of the system. Researchers and developers in the SET CPS project are now looking for new approaches to make the development processes for manufacturers and suppliers reliable and economical, and enable them to meet development times.

The project therefore aims to develop intelligent, simulation-based processes that improve and systematize the development and test process of complex vehicles and increase the degree of automation. For this purpose, design and testing are more closely interlinked to achieve a high level of quality even in the early development phases. The researchers also use the latest mathematical methods from multi-objective optimization, which is one of the core competencies of the Institute of Industrial Mathematics. This enables them to simultaneously achieve competing goals, such as energy efficiency, comfort, and costs, while ensuring the safety of the system. The plan is to integrate the new processes into the dSPACE tool chain and evaluate them using an example from e.GO vehicle development.

“As consortium leader of the project, our goal is to take the next step toward a one-stop development environment for autonomous vehicles," explained Dr. Rainer Rasche, Group Manager Test Automation at dSPACE. “The resulting tool chain enables the developer to adjust the parameters of an ECU to different, typical traffic situations and simultaneously test them in the simulated environments. This will enable our customers to accelerate their development."

Dr. Michael Riesener, Vice President Corporate Research at e.GO Mobile AG, said: “The simultaneous development and testing of new systems for our electric vehicles made possible by SET CPS also enables us to achieve fast development times and to design the vehicles with an even stronger focus on requirements. For this reason, we look forward to advancing the research project in cooperation with our partners."

About e.GO Mobile AG

e.GO Mobile AG was founded in 2015 by Prof Dr Günther Schuh as a manufacturer of electric vehicles. The more than 400 employees use the campus's unique network of research facilities and approximately 360 technology companies on the RWTH Aachen Campus. Highly agile teams work on a variety of cost-effective and customer-focused electric vehicles for short-haul traffic. e.GO Mobile AG is currently commissioning its new plant in Rothe Erde, Aachen, for series production.

www.e-go-mobile.com

About IFIM

The Institute of Industrial Mathematics was founded at the University of Paderborn to facilitate a direct transfer of knowledge from applied mathematics to business. Together with partners from industry, in particular small and medium-sized enterprises, they identify mathematical problems and develop efficient solutions that are based on the latest scientific findings. The interaction between science and industry can yield significant progress in scientific, economic, and technological terms.

About dSPACE

dSPACE develops and distributes integrated hardware and software tools for developing and testing electronic control units. As a one-stop supplier, dSPACE is a sought-after partner and solution provider in many development areas of the automotive industry, from electromobility to vehicle networking to autonomous driving. The company's customer base therefore includes virtually all major vehicle manufacturers and suppliers. dSPACE systems are also used in the aerospace and other industries. With more than 1,700 employees worldwide, dSPACE is headquartered in Paderborn, Germany; has three project centers in Germany; and serves customers through regional dSPACE companies in the USA, the UK, France, Japan, China, and Croatia.

For more information on the funding program, visit: https://www.leitmarktagentur.nrw/leitmarktwettbewerbe/ikt/

Our project: Understanding and utilising relationships between coherent structures and almost invariant sets in function space

Our research project: Multiobjective Optimal Control of Partial Differential Equations Using Reduced-Order Modeling 

Information-Based Optimization of Surgery Schedules

The health care sector is one of the most important economy branches in Germany which is subject to steadily increasing expenses over the last years. One of the main cost components are hospitals. In particular, operating rooms generate a huge portion of the hospitals expenses. In the future, a more efficient operation room management is needed to reduce operating cost and staff overtime to allow patient therapies of higher quality.

Project Description

The project Information-Based Optimization of Surgery Schedules (IBOSS) focuses on the development of new and efficient methods to improve the individual work- and patient flow in hospitals.  We work closely with our project partner Charité Berlin in order to bring new algorithmic concepts for difficult problems into practice. One part of the project includes the predictive analysis of activity durations to accurately model the involved sub-processes in a hospital. On that basis, we develop algorithms to compute optimized micro- and macro-level surgery schedules. The particular focus lies on the algorithmic treatment of stochastic influences on the planned schedule, such as operational delays and sudden emergencies. Our solution methodologies are based on the following techniques 

• Optimal learning of classificators in data analysis;
• Stochastic/robust resource-constrained project scheduling;
• Multiobjective Optimization and Stochastic Control of Markov Chains;
• Dynamic interplay between micro- and macro models.

The future goal is to integrate an adaptive self-learning optimization system that automatically recognizes variations and trends in a changing therapy evironment.  A further objective is the implementation of a first computational test and evaluation system for practical usage.

Multiobjective Optimization of Dynamic Operation Room Models

Besides determining an optimal schedule for operations, there are numerous additional factors that can influence the quality of operation planning. These are, for example, allocation of personnel and medication as well as starting times for the individual subtasks. The corresponding decisions can be made with respect to multiple, in general conflicting criteria, amongst which are the quality of the medical treatment, the ability to react to unforeseen events, the satisfaction of personnel as well as patients and economic factors. This requires the computation of the set of optimal compromises between these objectives, the so-called Pareto set.

The goal of the part of the project carried out in Paderborn is therefore to develop a dynamic model of the operating process which is then used in an optimization algorithm running in parallel to the real process. Hence, concurrent objectives which are subject to uncertainties as well as  real-time applicability have to be taken into account. Based on the current priorities, an operation planner can select an optimal compromise from the Pareto set. Furthermore, the results can be utilized to assist and enhance the task of operation scheduling.

Project Homepage: Information-Based Optimization of Surgery Schedules

Our research projects: Selbstoptimierung; Ressourceneffiziente selbstoptimierende Großwäscherei