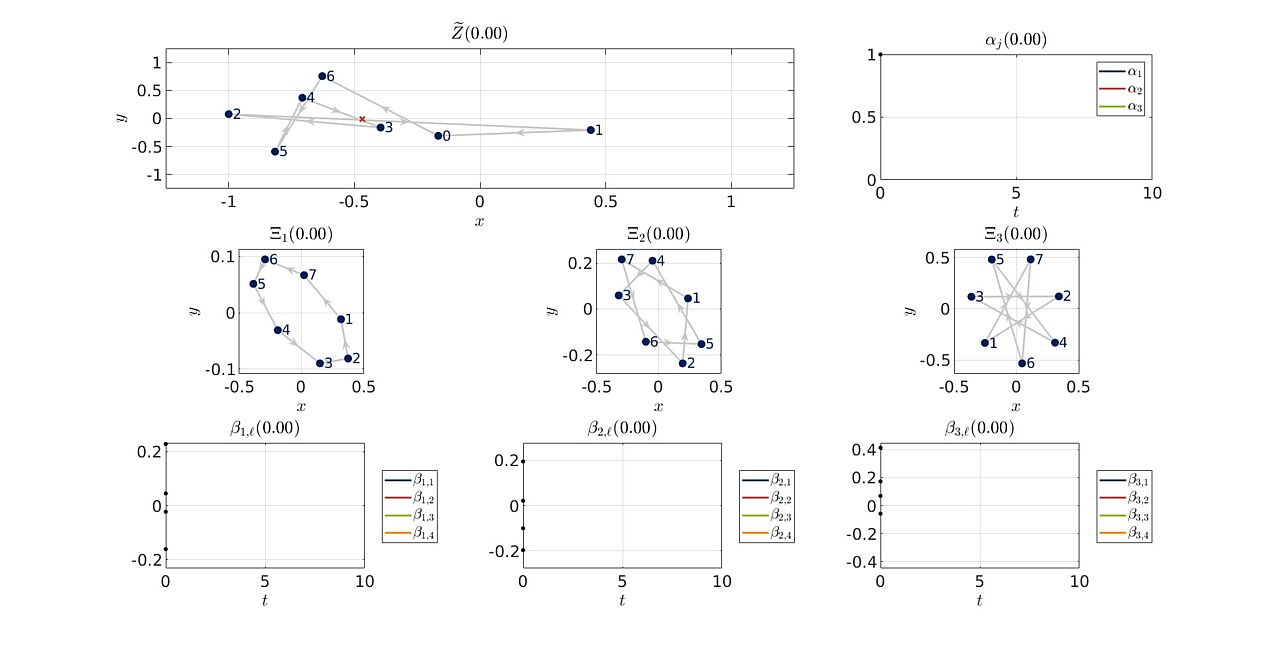
Infinite Dimensional Dynamical Systems
Development of a set-oriented numerical technique which allows to compute low-dimensional invariant sets for infinite dimensional dynamical systems.
Systems of interest:
- Delay Differential Equations (DDEs): type of differential equation in which the time derivative of the unknown function depends not only on the current state but also on previous times.
Focus of interest: Analysis of long term behavior of DDEs
Applications: e.g. signal processing, disease transition, population models - Partial Differential Equations (PDEs): type of differential equation in which the time derivative of the unknown function depends on multivariable functions and their partial derivatives.
Focus of interest: Analysis of long term behavior of PDEs
Applications: e. g. fluid dynamics, quantum mechanics, electrodynamics
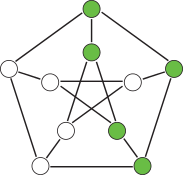
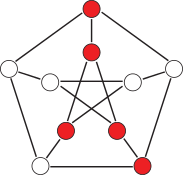
Networked systems
In engineering applications, one of the major challenges today is to develop reliable and robust control algorithms for complex net- worked systems. Controllability and observability of such systems play a crucial role in the design process. The underlying network structure may contain symmetries – caused, for example, by the cou- pling of identical building blocks – and these symmetries lead to repeated eigenvalues in a generic way. This complicates the design of controllers since repeated eigenvalues decrease the controllability of the system. We analyze the relationship between the controllability and observability of complex networked systems and symmetries using results from group representation theory.
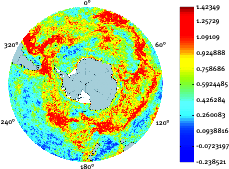
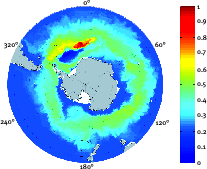
Ocean Dynamics
Time-dependent transport maps for the Southern Ocean are useful in many ways: they permit precise mass, heat and freshwater transport calculations for the Antartic Circumpolar Current.
Cooperations: University of New South Wales, Australia; Centre National de la Recherche Scientifique, Brest, France
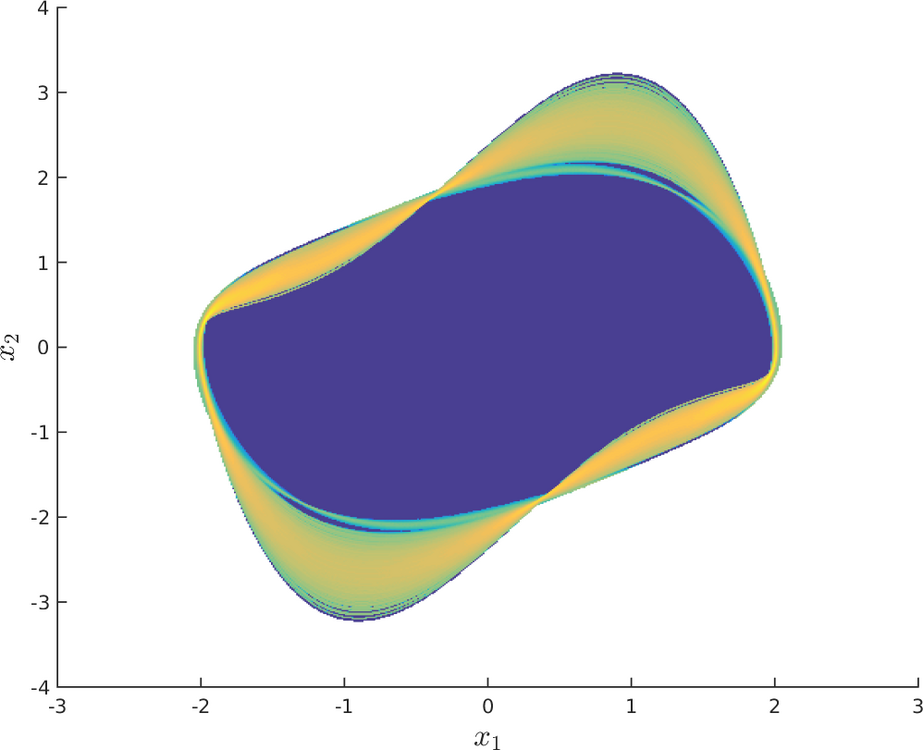
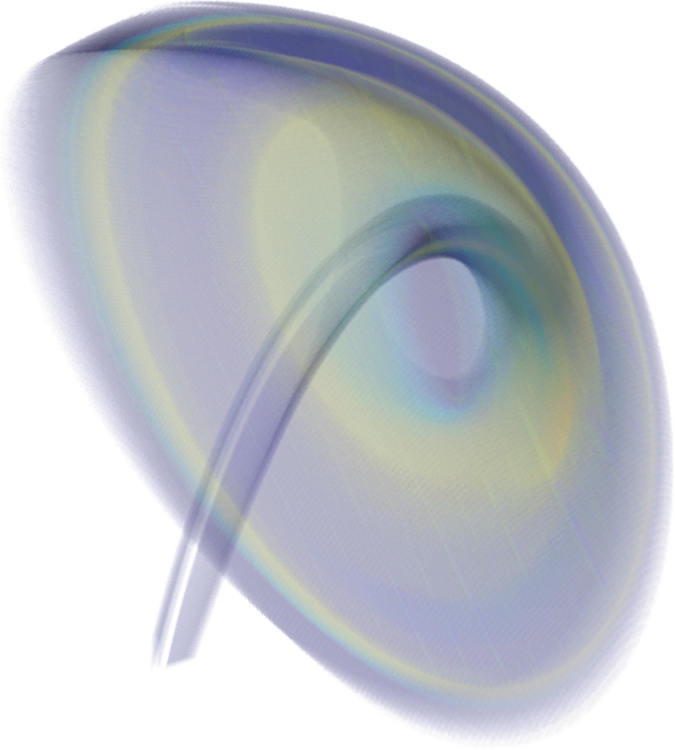
Uncertainty Quantification
Development of a set-oriented numerical methodology which allows to perform uncertainty quantification (UQ) for dynamical systems from a global point of view.
-
State space approach: Dynamical Systems with uncertain parameters
Focus of interest: Analysis of the statistical behavior of the system to capture the long-term uncertainty propagation
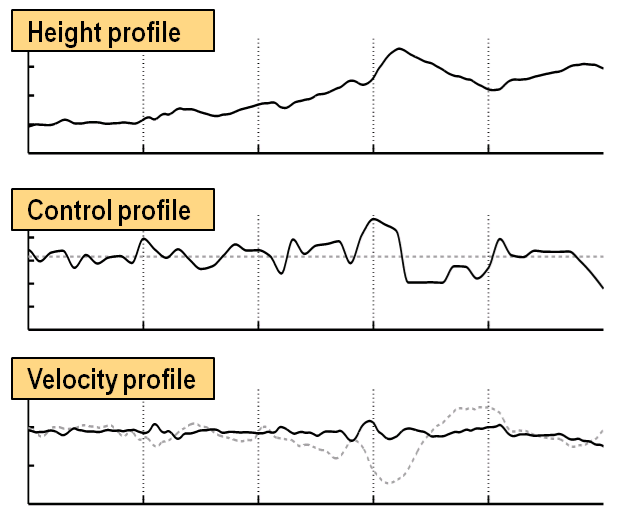
Swarm dynamics
Analysis of local, distributed strategies for swarms of mobile robots with techniques from dynamical systems research.
Multiobjective Optimization
Efficient solutions of multiobjective optimization problems and systems of nonlinear equations require new theory and algorithms. These problems can be of hierarchical structure or depend on additional parameters.
Cooperations: it's OWL - Intelligent Technical Systems Ostwestfalen Lippe; Hella KGaA Hueck & Co.
Publications
On the Dynamical Hierarchy in Gathering Protocols with Circulant Topologies
R. Gerlach, S. von der Gracht, M. Dellnitz, in: Lecture Notes in Computer Science, Springer Nature Switzerland, Cham, 2025.
Symmetry Preservation in Swarms of Oblivious Robots with Limited Visibility
R. Gerlach, S. von der Gracht, C. Hahn, J. Harbig, P. Kling, in: S. Bonomi, L. Galletta, Etienne Rivière, Valerio Schiavoni (Eds.), 28th International Conference on Principles of Distributed Systems (OPODIS 2024), Schloss Dagstuhl -- Leibniz-Zentrum für Informatik, 2025.
Analyzing Symmetries of Swarms of Mobile Robots Using Equivariant Dynamical Systems
R. Gerlach, S. von der Gracht, ArXiv:2503.07576 (2025).
Inertial dynamics with vanishing Tikhonov regularization for multobjective optimization
R.I. Bot, K. Sonntag, Journal of Mathematical Analysis and Applications (2025).
Homogeneous Coupled Cell Systems with High-dimensional Internal Dynamics
S. von der Gracht, E. Nijholt, B. Rink, ArXiv:2510.06740 (n.d.).
First-order methods and gradient dynamical systems for multiobjective optimization
K. Sonntag, First-Order Methods and Gradient Dynamical Systems for Multiobjective Optimization, Paderborn University, 2025.
A note on the convergence of deterministic gradient sampling in nonsmooth optimization
B. Gebken, Computational Optimization and Applications (2024).
Fast Multiobjective Gradient Methods with Nesterov Acceleration via Inertial Gradient-Like Systems
K. Sonntag, S. Peitz, Journal of Optimization Theory and Applications (2024).
A Descent Method for Nonsmooth Multiobjective Optimization in Hilbert Spaces
K. Sonntag, B. Gebken, G. Müller, S. Peitz, S. Volkwein, ArXiv:2402.06376 (2024).
Heteroclinic dynamics in network dynamical systems with higher-order interactions
C. Bick, S. von der Gracht, Journal of Complex Networks 12 (2024).
Show all publications