Willkommen auf der Homepage der Arbeitsgruppe Computeralgebra und Zahlentheorie
Conference: "Arithmetic Statistics" - August 24-28, 2026
Inverse problems in number theory are refined by studying their quantitative counterparts. Typical examples are the distribution of Galois groups and class groups of number fields, whose behavior is predicted by celebrated conjectures of Malle and Cohen—Lenstra—Martinet. Analogous questions for function fields have received much attention, including the case that the characteristic divides the group order.
The purpose of this workshop is to offer the opportunity to present recent results in this area and to have plenty of time for collaboration.
The conference "Arithmetic Statistics" will take place at the Institute of Mathematics in Paderborn (Germany) . Please apply here.
Link to Website: Conference: "Arithmetic Statistics"
Alles auf einen Blick
Nachrichten
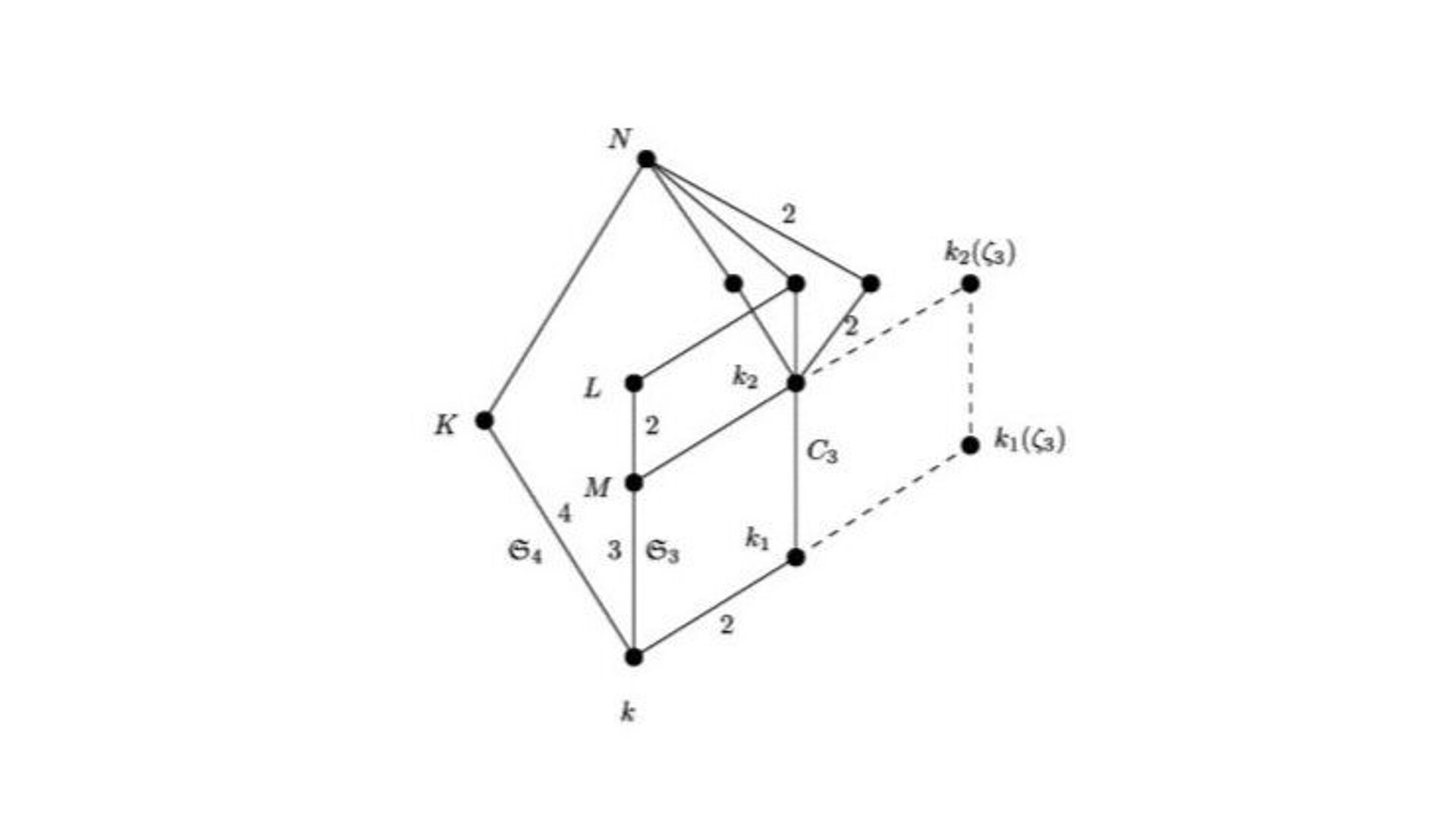
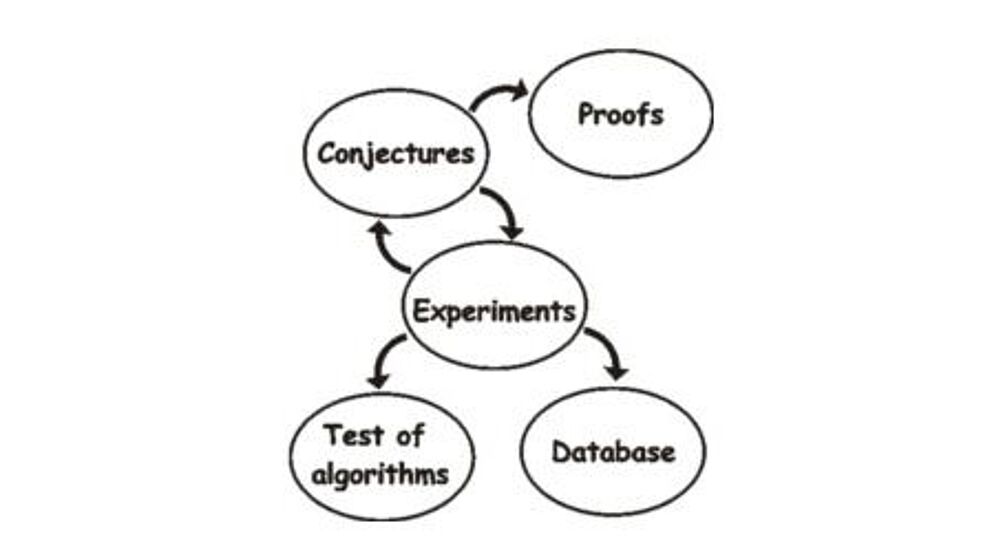
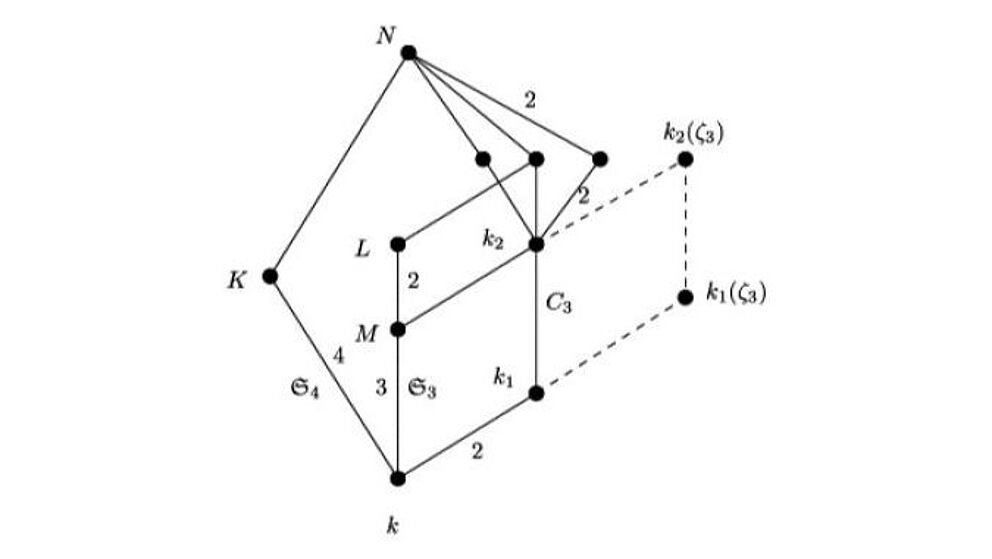
Das wesentliche Ziel der Computeralgebra ist es, mathematische Probleme möglichst symbolisch auf dem Computer abzubilden und effizient zu lösen. Hierzu werden einerseits neue Algorithmen theoretisch entwickelt und untersucht, andererseits werden sie in bestehende Computeralgebrasysteme wie Kant oder Magma implementiert. Die algorithmischen und theoretischen Hauptentwicklungen finden im Bereich der Galois- und Zahlentheorie statt. Seit mehreren Jahren wird via Web-Interface eine Datenbank für Zahlkörper zur Verfügung gestellt, die mehr als 3 Millionen Körper mit „interessanten“ Galoisgruppen enthält. Die entwickelten Algorithmen, sowie hiermit berechnete Daten werden benutzt, um Vermutungen für mathematische Probleme aufzustellen oder experimentell zu verifizieren. Mehrere Mitglieder der Arbeitsgruppe arbeiten an sogenannten asymptotischen Fragestellungen, wie etwa der Verteilung von Körpern mit vorgegebener Galoisgruppe oder der Verteilung von Klassengruppen algebraischer Zahlkörper. Hierbei erweist es sich als sehr nützlich, dass man mit dem Computer Experimente durchführen kann.