Welcome to the homepage of the Research Group Computer Algebra and Number Theory
Everything at a glance
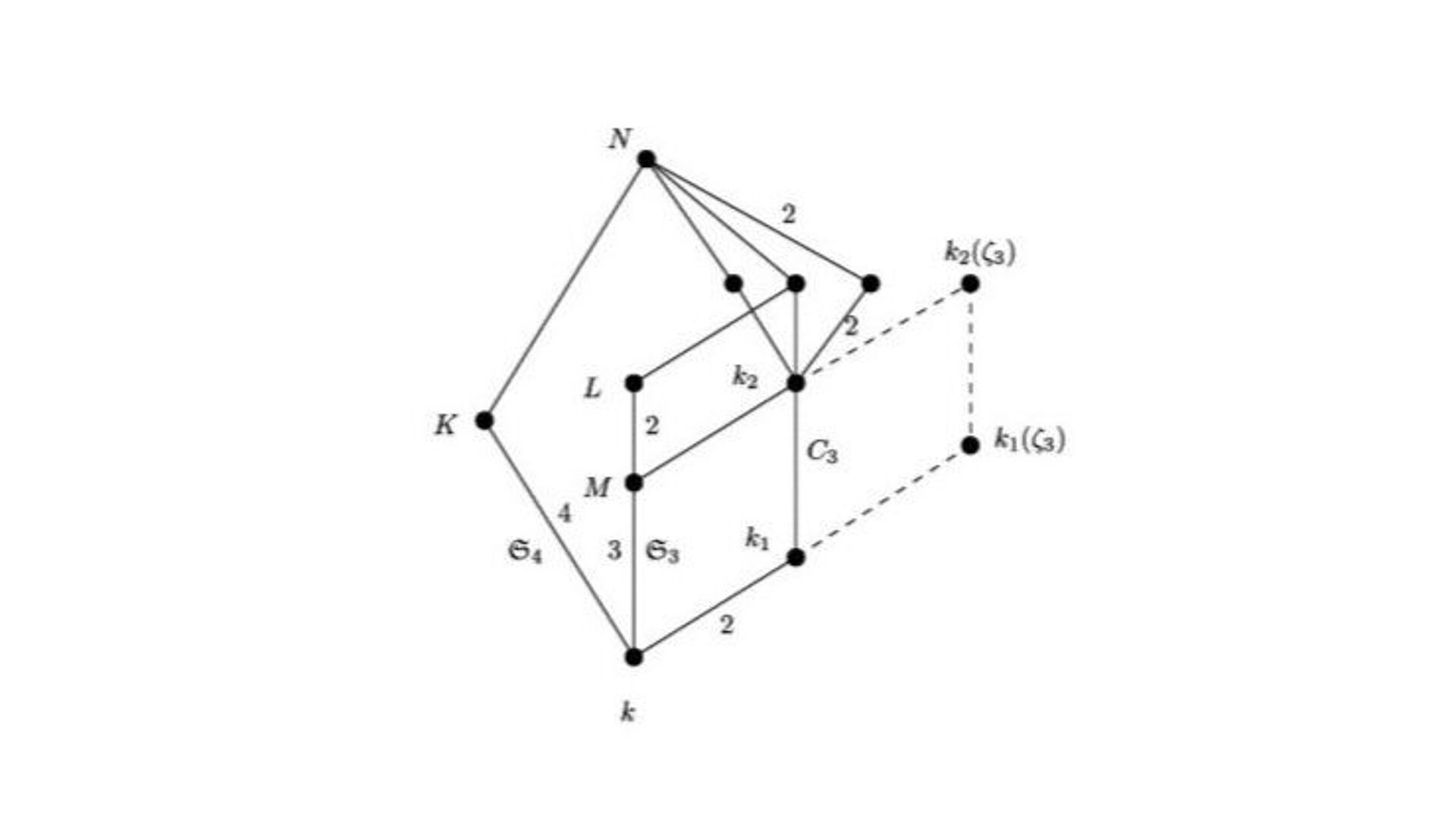
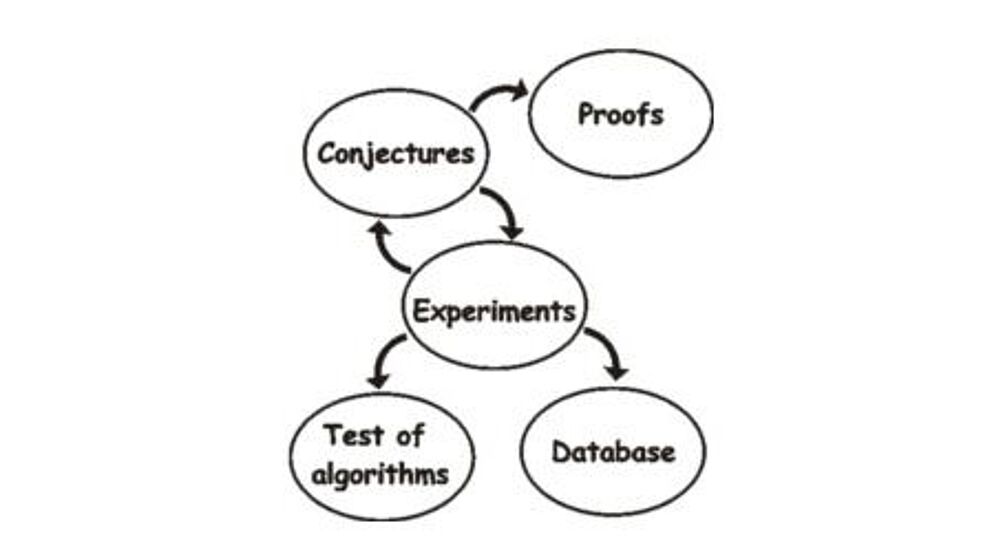
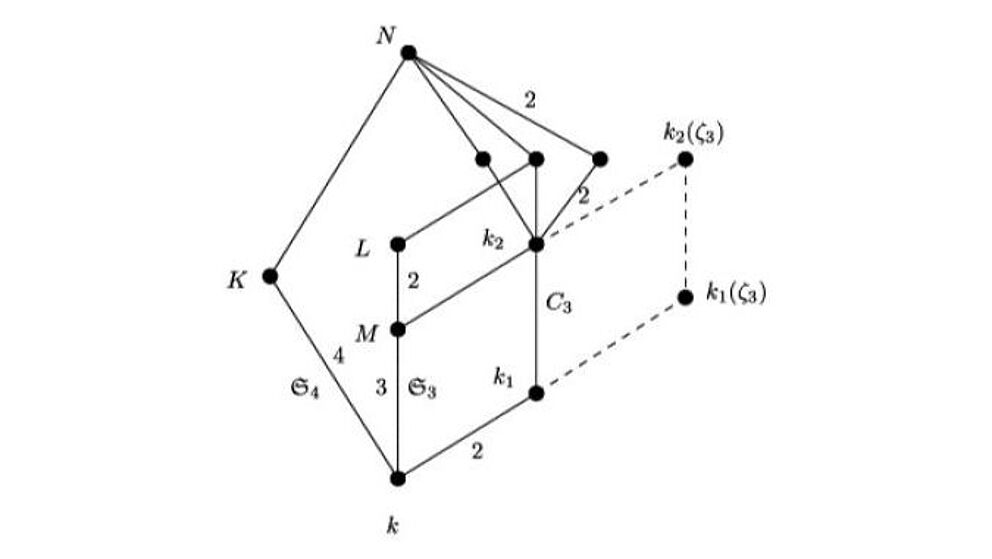
The main goal of computer algebra is the symbolic solution of mathematical problems on a computer. Therefore, on the one hand, new algorithms are theoretically developed and reviewed and on the other hand implemented into existing computer algebra systems, like Kant or Magma. For many years, a database for number fields has been provided via web-interface, which contains of more than 3 million number fields with "interesting" Galois groups. The developed algorithms and its calculated data are used to establish hypotheses for mathematical problems or to verify them experimentally. Several members of our work group are working on so called asymptotic problems, e.g. the distribution of fields with a given Galois group or the distribution of class groups in algebraic (of algebraic) number fields. In this case, using the computer for experiments has turned out to be very useful.