Professor Dr. Michael Dellnitz

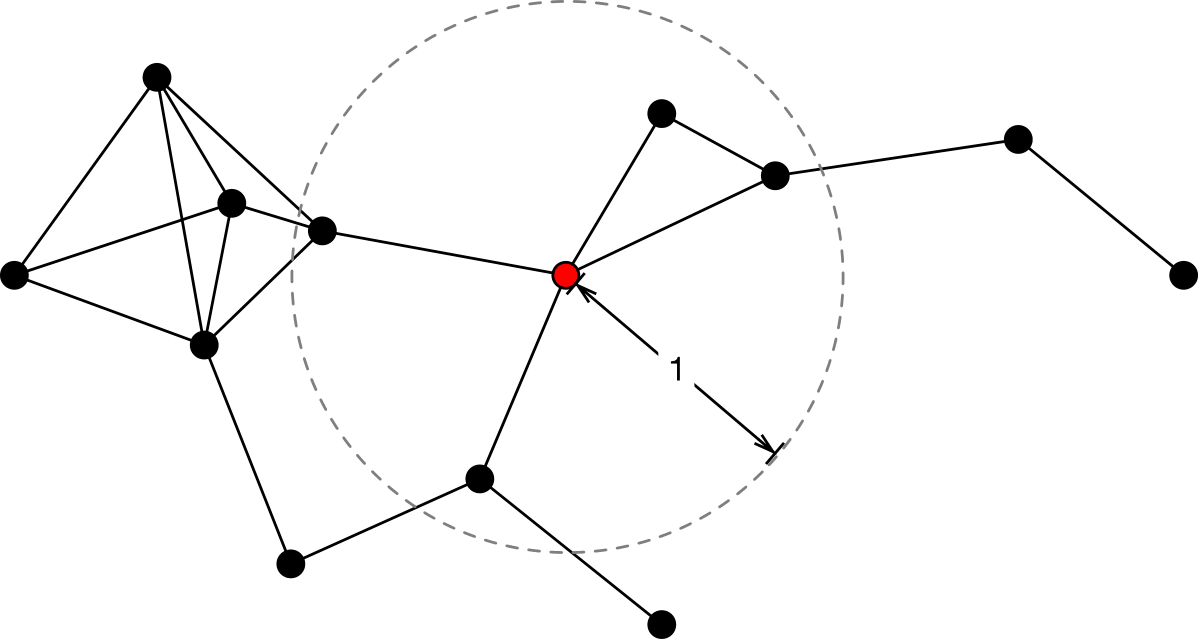
Das Ziel dieses Projekts ist es, die Möglichkeiten und Grenzen lokaler, verteilter Strategien für Schwärme mobiler Roboter zu untersuchen. Solche Strategien bestehen aus Protokollen, die von den einzelnen Robotern ausgeführt werden. Sie sollen die Bewegungen der Roboter so lenken, dass aus einer beliebigen Ausgangskonfiguration der Roboter global eine vorgegebene Formation wie das Sammel, die Linienbildung oder andere Formen erreicht wird. Diese Forschungsrichtung ist im "Distributed Computing" etabliert. Unser Ansatz besteht darin, Techniken aus dem Distributed Computing und der Theorie der dynamischer Systeme zu kombinieren, um das Verständnis von Protokollen für solche Formationsaufgaben zu verbessern. Dazu analysieren wir die Geschwindigkeit der Protokolle hinsichtlich Laufzeitkomplexität im Sinne des Distributed Computing sowie Stabilitätseigenschaften der vorgeschriebenen Formation unter Verwendung von Ideen dynamischer Systeme. Während in der Distributed-Computing-Community oft nur eine Worst-Case-Analyse betrachtet wird, erlauben die Werkzeuge dynamischer Systeme eine feinere Analyse der Eingangskonfigurationen durch die Untersuchung des Zustandsraums. Konkreter beschreibt die "State-Space-Foliation" das langfristige dynamische Verhalten von Eingabekonfigurationen detaillierter, d.h. sie erlaubt es, Klassen von Konfigurationen zu identifizieren, die vergleichsweise schnell oder langsam konvergieren, und sogar Klassen, die nicht zur vorgeschriebenen Formation konvergieren. Somit führt die Kombination beider Sichtweisen zu einem tieferen Verständnis verteilter Strategien für Schwärme mobiler Roboter.

Unser Forschungsprojekt: Multiobjective Optimization of Non-Smooth PDE-Constrained Problems - Switches, State Constraints and Model Order Reduction

Simultanes Entwickeln und Testen von Cyber Physical Systems (CPS) am Anwendungsbeispiel eines elektrisch angetriebenen autonomen Fahrzeugs

dSPACE, e.GO Mobile und Institut für Industriemathematik starten Forschungsprojekt
 

Wie können autonome Fahrzeuge mit Elektroantrieb als Beispiele für komplexe cyber-physische Systeme schneller, kostengünstiger und ressourcenschonender entwickelt werden? Und wie lässt sich die Sicherheit solcher Fahrzeuge auf der Straße erhöhen? Ein Team aus Forschern und Entwicklern von dSPACE, der e.GO Mobile AG und dem Institut für Industriemathematik der Universität Paderborn hat vor einigen Wochen ein Forschungsprojekt gestartet, um diese komplexe Fragestellung zu beantworten. Das Projekt wird im Rahmen des Leitmarktwettbewerbs IKT.NRW mit Mitteln des Landes NRW und der EU gefördert. „Simultanes Entwickeln und Testen von Cyber Physical Systems (CPS) am Anwendungsbeispiel eines elektrisch angetriebenen autonomen Fahrzeugs – SET CPS“ lautet der offizielle Titel des Projektes mit einer Laufzeit von 36 Monaten.

Bei der Entwicklung von Fahrzeugen sorgen Trends wie das automatisierte Fahren oder die Entwicklung alternativer Antriebe, wie zum Beispiel batteriebetriebene Fahrzeuge, für einen sprunghaften Anstieg der Anforderungen an die zugrunde liegenden Systeme. Bei der Entwicklung solcher Fahrzeuge geht es darum, eine Vielzahl an Zielgrößen wie Verbrauch, Reichweite und Fahrkomfort zu optimieren und die Sicherheit des Systems zu garantieren. Um die Entwicklungsprozesse für Hersteller und Zulieferer verlässlich und ökonomisch zu gestalten und Entwicklungszeiten einhalten zu können, machen sich Forscher und Entwickler im Projekt SET CPS jetzt auf die Suche nach neuen Ansätzen.

Im Projekt sollen daher intelligente, simulationsbasierte Verfahren entwickelt werden, die den Entwicklungs- und Testprozess komplexer Fahrzeuge verbessern, systematisieren und den Automatisierungsgrad erhöhen. Dazu werden die Auslegung und der Test enger miteinander verzahnt, um bereits in frühen Entwicklungsphasen einen hohen Qualitätsgrad zu erreichen. Hierzu kommen neueste mathematische Methoden aus der Mehrzieloptimierung zum Einsatz, die einer der Kernkompetenzen des Instituts für Industriemathematik ist. So können miteinander konkurrierende Ziele wie Energieeffizienz, Komfort und Kosten gleichzeitig berücksichtigt und darüber hinaus die Sicherheit des Systems gewährleistet werden. Geplant ist, die neuen Verfahren in die Toolkette von dSPACE zu integrieren und anhand eines Beispiels aus der Fahrzeugentwicklung von e.GO zu evaluieren.

„Als Konsortialführer des Projektes ist es unser Ziel, den nächsten Schritt hin zu einer Entwicklungsumgebung aus einer Hand für autonome Fahrzeuge zu machen“, erklärte Dr. Rainer Rasche, Group Manager Test Automation bei dSPACE. „Die entstehende Toolkette ermöglicht dem Entwickler, die Parameter eines Steuergerätes auf verschiedene, typische Verkehrssituationen auszulegen und gleichzeitig in den simulierten Umgebungen zu testen. So können unsere Kunden ihre Entwicklung beschleunigen.“

Dr. Michael Riesener, Vice President Corporate Research bei der e.GO Mobile AG, sagte: „Das durch SET CPS ermöglichte simultane Entwickeln und Testen neuer Systeme für unsere elektrischen Fahrzeuge befähigt uns weiterhin, schnelle Entwicklungszeiten zu realisieren und die Fahrzeuge noch anforderungsorientierter auszulegen. Aus diesem Grund freuen wir uns darauf, das Forschungsprojekt gemeinsam mit unseren Partnern voranzutreiben.“

Über e.GO Mobile AG

Die e.GO Mobile AG wurde 2015 von Prof. Dr. Günther Schuh als Hersteller von Elektrofahr-zeugen gegründet. Auf dem RWTH Aachen Campus nutzen die mehr als 450 Mitarbeiter das einzigartige Netzwerk des Campus mit seinen Forschungseinrichtungen und ca. 360 Technologieunternehmen. In agilen Teams wird an verschiedenen kostengünstigen und kundenorientierten Elektrofahrzeugen für den Kurzstreckenverkehr gearbeitet. Die Serienproduktion des e.GO Life ist im März 2019 im neuen e.GO Werk in Aachen Rothe Erde angelaufen.

www.e-go-mobile.com

Über IFIM

Das Institut für Industriemathematik wurde an der Universität Paderborn gegründet, um einen direkten Transfer aus der angewandten Mathematik in die Wirtschaft zu vereinfachen. Gemeinsam mit Partnern aus der Industrie, insbesondere dem Mittelstand, werden mathematische Problemstellungen identifiziert und effiziente Lösungsverfahren erarbeitet, die auf dem neuesten Stand der Wissenschaft beruhen. Durch das Zusammenwirken von Wissenschaft und Wirtschaft können sowohl in wissenschaftlicher als auch in wirtschaftlicher und technologischer Hinsicht signifikante Fortschritte erzielt werden.

Über dSPACE

dSPACE entwickelt und vertreibt integrierte Hardware- und Software-Werkzeuge für die Entwicklung und den Test von Steuergeräten. Als Komplettanbieter ist dSPACE ein gefragter Partner und Lösungsanbieter in vielen aktuellen Entwicklungsbereichen der Automobilindustrie, von der Elektromobilität über die automobile Vernetzung bis hin zum autonomen Fahren. Zum Kundenstamm gehören daher auch nahezu alle namhaften Automobilhersteller und -zulieferer. Darüber hinaus werden dSPACE Systeme auch in der Luft- und Raumfahrt sowie in anderen Industriebereichen erfolgreich eingesetzt. Mit mehr als 1.700 Mitarbeitern weltweit ist dSPACE am Stammsitz in Paderborn, mit drei Projektzentren in Deutschland sowie durch Landesgesellschaften in den USA, Großbritannien, Frankreich, Japan, China und Kroatien vertreten.

Informationen zum Förderprogramm unter: https://www.leitmarktagentur.nrw/leitmarktwettbewerbe/

Unser Forschungsprojekt: Understanding and utilising relationships between coherent structures and almost invariant sets in function space

Unser Forschungsprojekt: Mehrziel-Optimalsteuerung partieller Differentialgleichungen mittels Modellreduktion

Informationsbasierte Optimierung von Operationsplänen / Information-Based Optimization fo Surgery Schedules
 

In Deutschland ist der Gesundheitssektor einer der wichtigsten Wirtschaftszweige, der stetig steigenden Ausgaben unterliegt. Dabei beanspruchen Krankenhäuser und insbesondere Operationssäle einen großen Anteil dieser Kosten. Um die Patienten besser zu versorgen sowie die Operationskosten und die Überstunden zu reduzieren, wir daher eine effizientere Verwaltung der Operationssäle benötigt.

Projektbeschreibung
 

In dem Projekt Information-Based Optimization of Sugery Schedules (IBOSS) wird an der Entwicklung von neuen effizienten Methoden zur Verbesserung des Arbeits- und Patientenflusses in Krankenhäusern geforscht. Zur Entwicklung dieser Konzepte und Algorithmen arbeiten wir eng mit unserem Projektpartner Charité Berlin zusammen. Ein Teil des Projektes ist die vorausschauende Analyse der beteiligten Teilprozesse in einem Krankenhaus, damit diese genau modelliert werden können. Auf dieser Grundlage entwickeln wir Algorithmen für die Berechnung von Operationsplänen, bei denen sowohl auf einer Mikro- als auch auf einer Makroebene Optimierungen durchgeführt werden. Ein besonderes Augenmerk liegt dabei auf der algorithmische Behandlung von stochastischen Einflüssen wie Verzögerungen innerhalb einer Operation oder plötzliche Notfälle. Die Lösungsansätze basieren auf folgende Techniken:

• Optimales Lernen von Klassifikatoren in der Datenanalyse

• Stochatische/Robuste Ressourcengebundene Projektplanung

• Mehrzieloptimierung und Optimalsteuerung von Markov-Prozessen

Das Ziel ist es, ein adaptives, selbst-lernendes Optimierungssystem zu entwickeln, welches automatisch Abweichungen und Entwicklungen innerhalb der sich verändernden Operationssal-Umgebung erkennt. Abschließend soll ein erster Prototyp des Systems in der praktischen Anwendung getestet und validiert werden.

Teilprojekt „Mehrzieloptimierung von dynamischen Modellen für Operationssäle“
 

Neben der Reihenfolge von Operationen gibt es viele weitere Faktoren, die die Qualität von Operationsplänen beeinflussen. Diese sind zum Beispiel die Verteilung des Personals und der Medikamente sowie die Startzeiten der einzelnen Operationsschritte. Die entsprechenden Entscheidungen haben Einfluss auf mehrere, meist zueinander in Konflikt stehende Zielfunktionen. Darunter befinden sich die Qualität der medizinischen Behandlung, die Möglichkeit, auf unerwartete Ereignisse zu reagieren, die Zufriedenheit des Personals und der Patienten sowie wirtschaftliche Faktoren. Hier muss demnach die Menge der optimalen Kompromisse zwischen dieser Kriterien, die so genannte Pareto-Menge, berechnet werden.

Das Ziel des Paderborner Teilprojektes ist daher, ein dynamisches Modell des Operationsprozesses zu entwickeln, welches dann in einem Optimierungsalgorithmus, der parallel zu dem realen Prozess arbeitet, eingesetzt wird. Dabei müssen konkurrierende Ziele sowie Unsicherheiten in Betracht gezogen werden. In Abhängigkeit von der aktuellen Situation kann ein Operationsplaner dann einen optimalen Kompromiss aus der Pareto-Menge auswählen. Darüber hinaus können die Ergebnisse für die Verbesserung der gesamten Operationsplanung verwendent werden.

IBOSS ist eine Kooperation mit den folgenden Institutionen: Zuse Institut Berlin (ZIB), FU Berlin, Charité

 Projekt-Homepage: Information-Based Optimization of Surgery Schedules

Unsere Forschungsprojekte: Selbstoptimierung; Ressourceneffiziente selbstoptimierende Großwäscherei