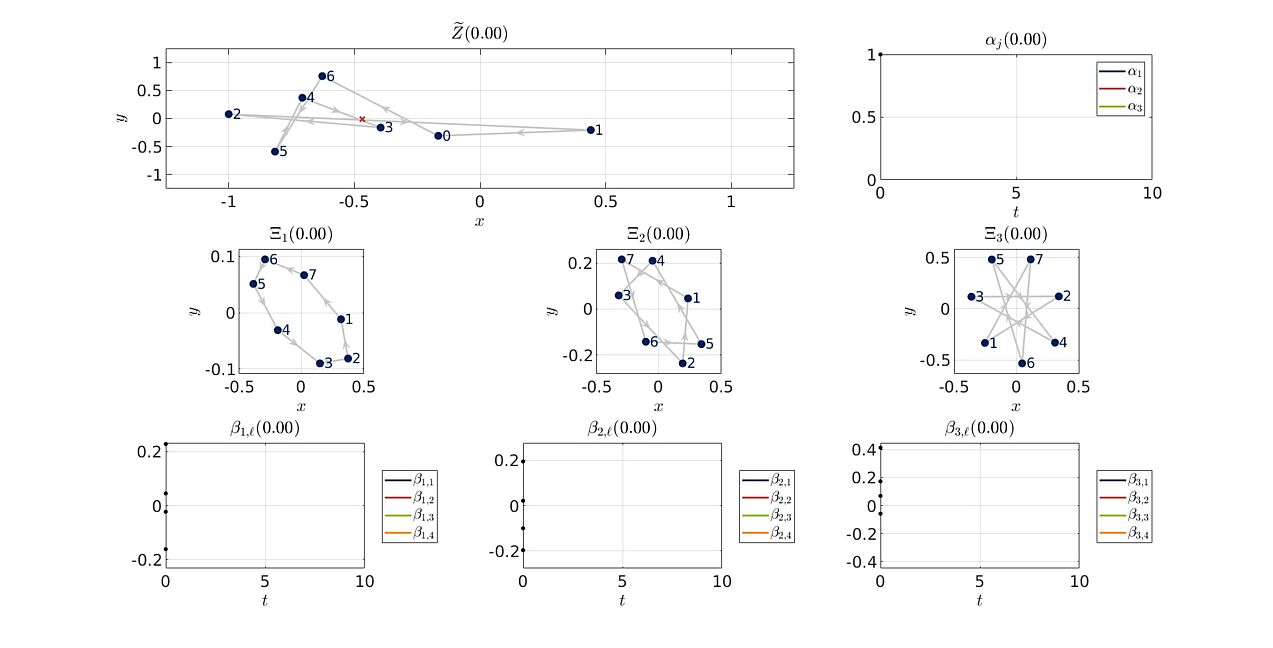
Unendlichdimensionale Dynamische Systeme
Entwicklung mengenorientierter Verfahren zur Berechnung von niedrigdimensionalen invarianten Mengen unendlichdimensionaler dynamischer Systeme.
Betrachtete Systeme:
- Delay Differentialgleichungen (DDEs): Differentialgleichungen, deren Ableitung nach Zeit sowohl vom aktuellen Zustand als auch von Zuständen aus der Vergangenheit abhängt.
Schwerpunkt: Analyse des Langzeitverhaltens von DDEs
Anwendungen: z.B. Signalverarbeitung, Bevölkerungsmodelle - Partielle Differentialgleichungen (PDEs): Differentialgleichungen, deren Ableitung nach Zeit sowohl von der Funktion als auch deren partiellen Ableitungen abhängt.
Schwerpunkt: Analyse des Langzeitverhaltens von PDEs
Anwendungen: z. B. Fluiddynamik, Quantenmechanik, Elektrodynamik
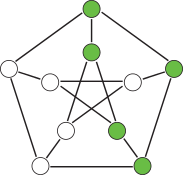
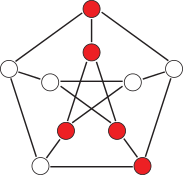
Networked systems
In engineering applications, one of the major challenges today is to develop reliable and robust control algorithms for complex net- worked systems. Controllability and observability of such systems play a crucial role in the design process. The underlying network structure may contain symmetries – caused, for example, by the cou- pling of identical building blocks – and these symmetries lead to repeated eigenvalues in a generic way. This complicates the design of controllers since repeated eigenvalues decrease the controllability of the system. We analyze the relationship between the controllability and observability of complex networked systems and symmetries using results from group representation theory.
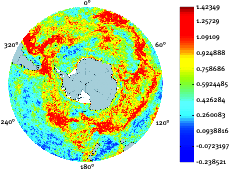
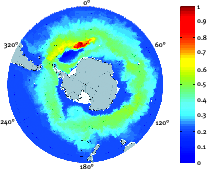
Ocean Dynamics
Time-dependent transport maps for the Southern Ocean are useful in many ways: they permit precise mass, heat and freshwater transport calculations for the Antartic Circumpolar Current.
Cooperations: University of New South Wales, Australia; Centre National de la Recherche Scientifique, Brest, France
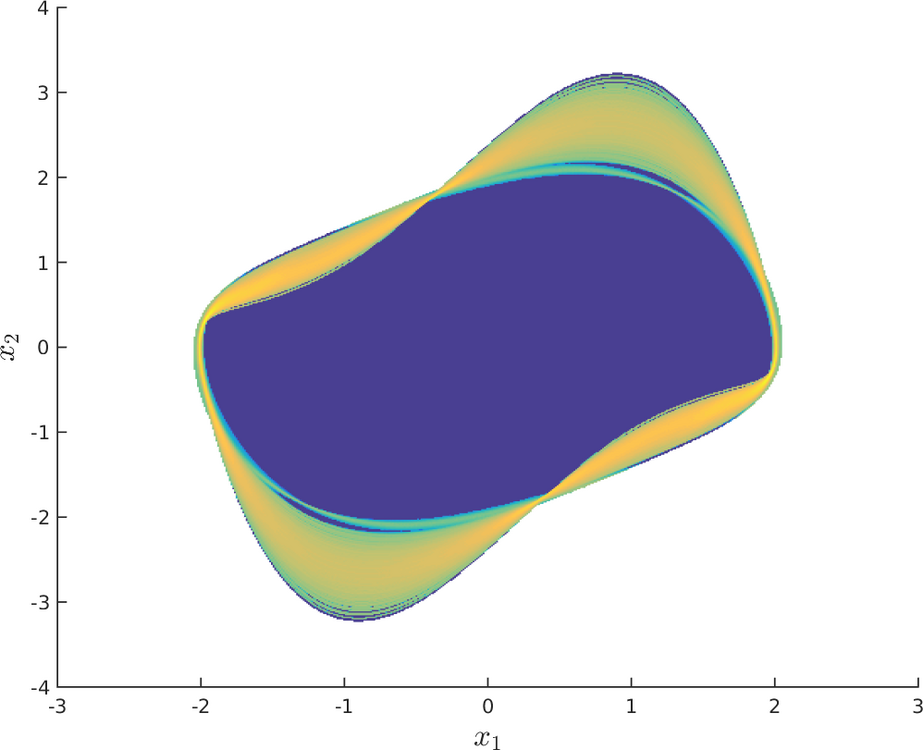
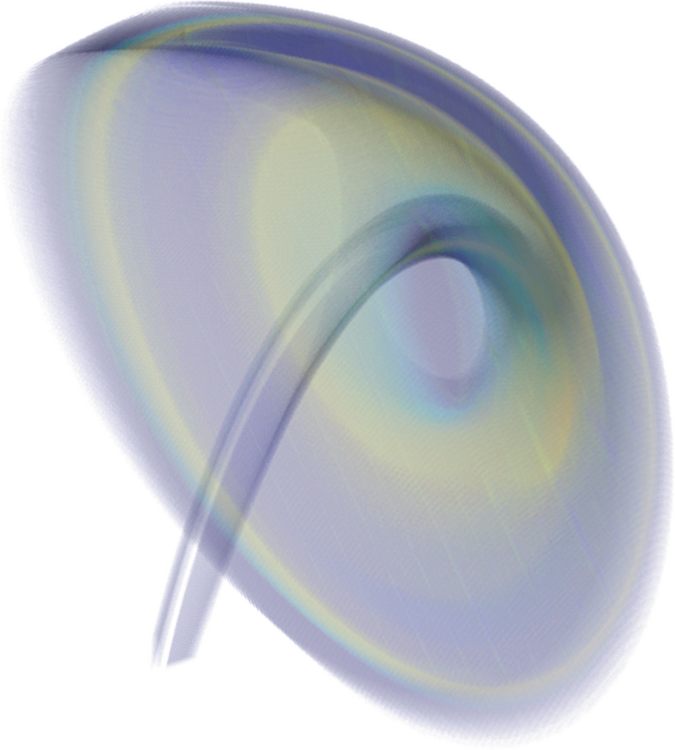
Uncertainty Quantification
Entwicklung mengenorientierter Verfahren zur globalen Analyse dynamischer Systeme mit Unsicherheiten.
-
Analyse im Zustandsraum: Dynamische Systeme mit Parameterunsicherheiten
Schwerpunkt: Globale Analyse des statistischen Verhaltens
Schwarmdynamik
Analyse von lokaler verteilter Strategien für Schwärme mobiler Roboter mittels Methoden der dynamischen Systeme.
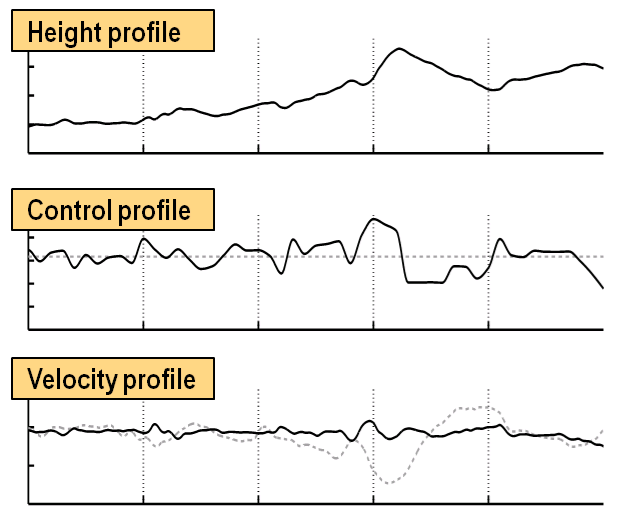
Mehrzieloptimierung
Effizientes Lösen von Mehrzieloptimierungsproblemen erfordert die Entwicklung neuer Algorithmen und Theoretischer Grundlagen. Diese Mehrzieloptimierungsprobleme können von hierarchischer Struktur sein oder von zusätzlichen Parametern abhängen.
Kooperationen: it's OWL - Intelligente Technische Systeme Ostwestfalen Lippe; Hella KGaA Hueck & Co.
Publikationen
On the Dynamical Hierarchy in Gathering Protocols with Circulant Topologies
R. Gerlach, S. von der Gracht, M. Dellnitz, in: Lecture Notes in Computer Science, Springer Nature Switzerland, Cham, 2025.
Symmetry Preservation in Swarms of Oblivious Robots with Limited Visibility
R. Gerlach, S. von der Gracht, C. Hahn, J. Harbig, P. Kling, in: S. Bonomi, L. Galletta, Etienne Rivière, Valerio Schiavoni (Eds.), 28th International Conference on Principles of Distributed Systems (OPODIS 2024), Schloss Dagstuhl -- Leibniz-Zentrum für Informatik, 2025.
Analyzing Symmetries of Swarms of Mobile Robots Using Equivariant Dynamical Systems
R. Gerlach, S. von der Gracht, ArXiv:2503.07576 (2025).
Inertial dynamics with vanishing Tikhonov regularization for multobjective optimization
R.I. Bot, K. Sonntag, Journal of Mathematical Analysis and Applications (2025).
Homogeneous Coupled Cell Systems with High-dimensional Internal Dynamics
S. von der Gracht, E. Nijholt, B. Rink, ArXiv:2510.06740 (n.d.).
First-order methods and gradient dynamical systems for multiobjective optimization
K. Sonntag, First-Order Methods and Gradient Dynamical Systems for Multiobjective Optimization, Paderborn University, 2025.
A note on the convergence of deterministic gradient sampling in nonsmooth optimization
B. Gebken, Computational Optimization and Applications (2024).
Fast Multiobjective Gradient Methods with Nesterov Acceleration via Inertial Gradient-Like Systems
K. Sonntag, S. Peitz, Journal of Optimization Theory and Applications (2024).
A Descent Method for Nonsmooth Multiobjective Optimization in Hilbert Spaces
K. Sonntag, B. Gebken, G. Müller, S. Peitz, S. Volkwein, ArXiv:2402.06376 (2024).
Heteroclinic dynamics in network dynamical systems with higher-order interactions
C. Bick, S. von der Gracht, Journal of Complex Networks 12 (2024).
Alle Publikationen anzeigen