Geometric flows and surface PDEs
PDEs with dynamic boundary conditions
Adaptivity for surface PDEs
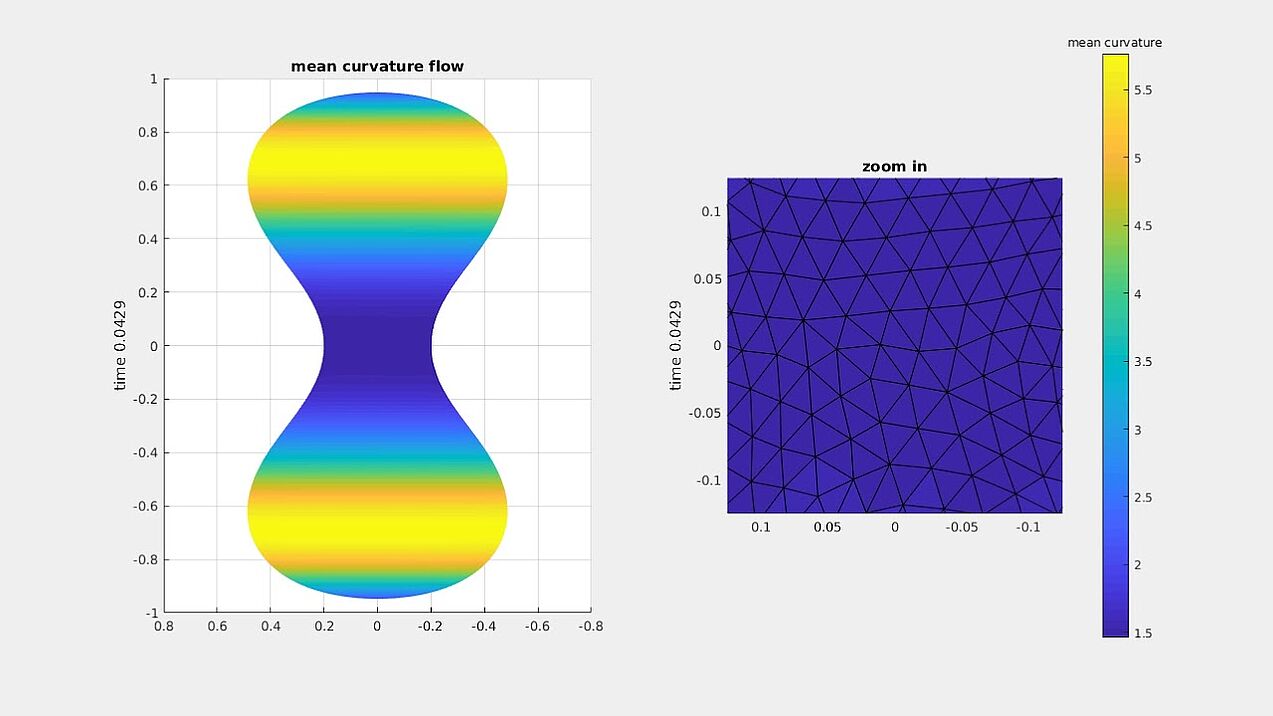
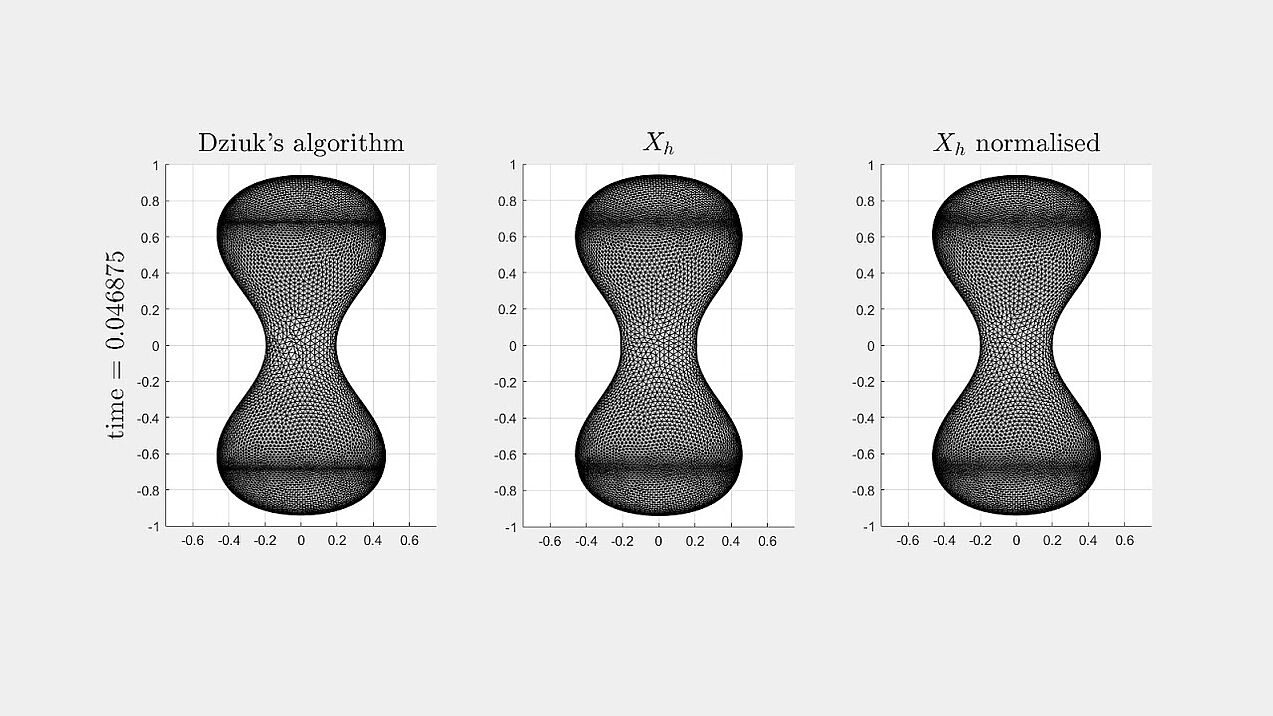
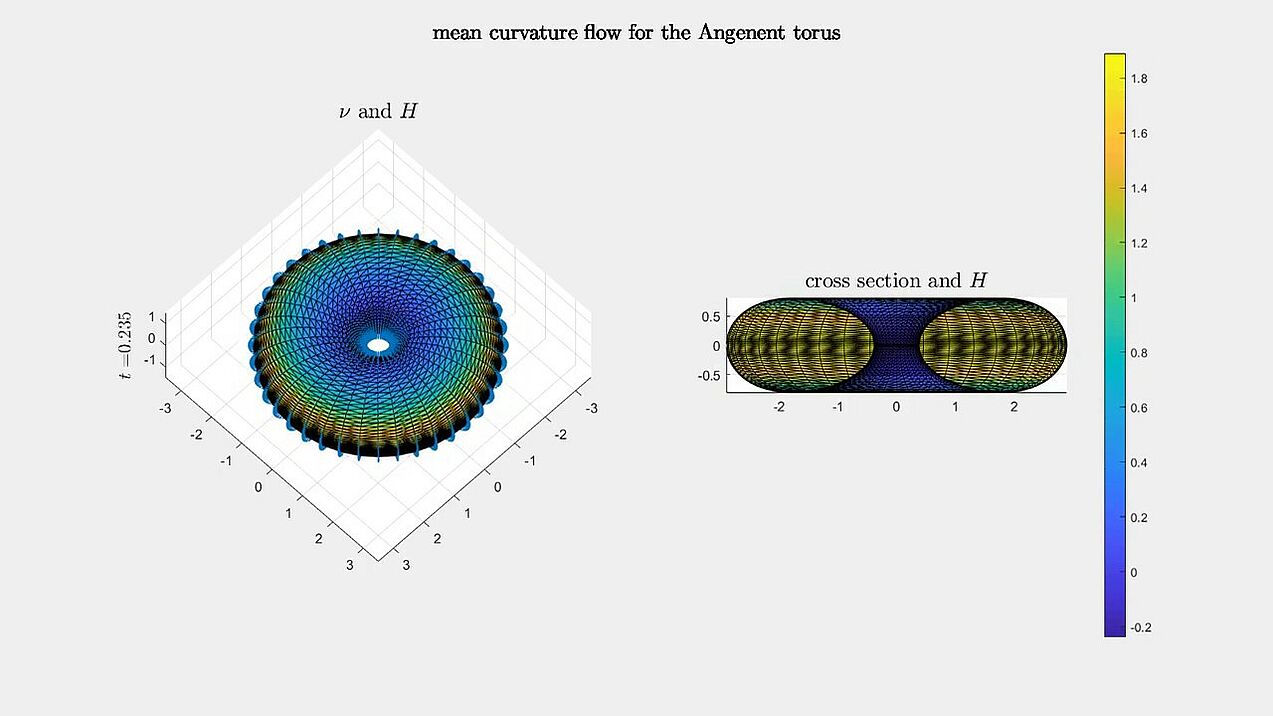
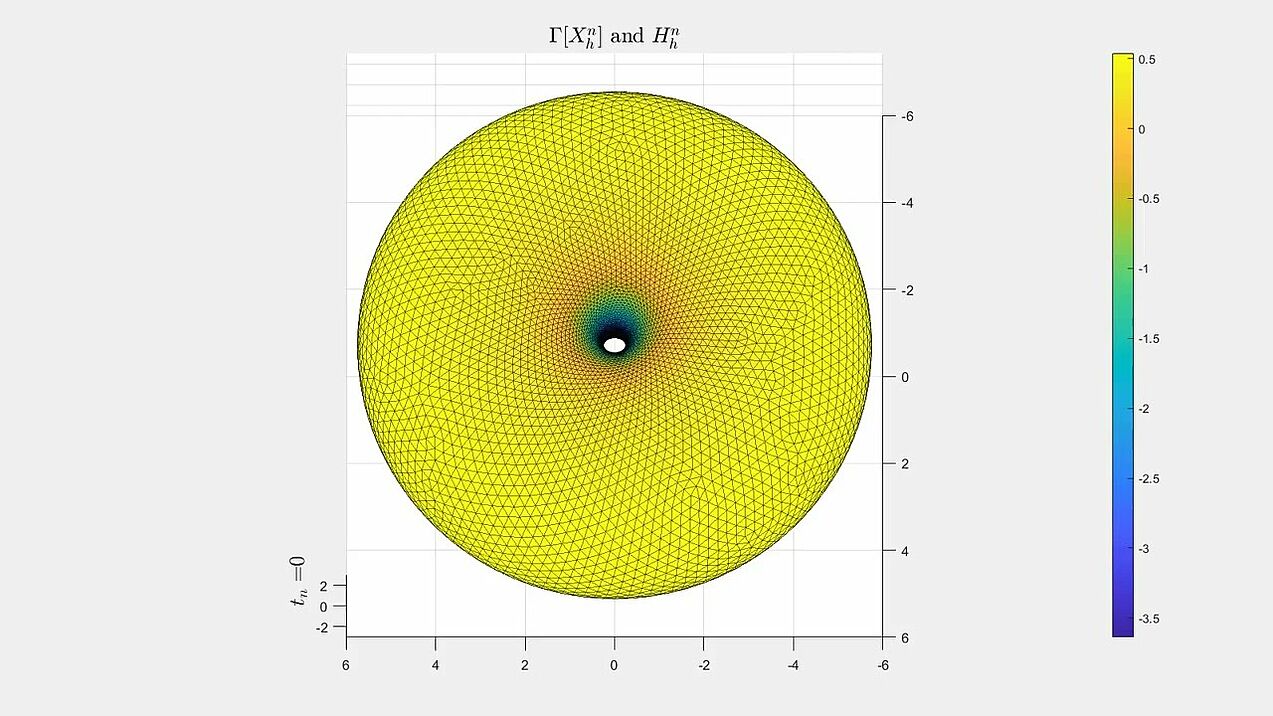
Mean curvature flow
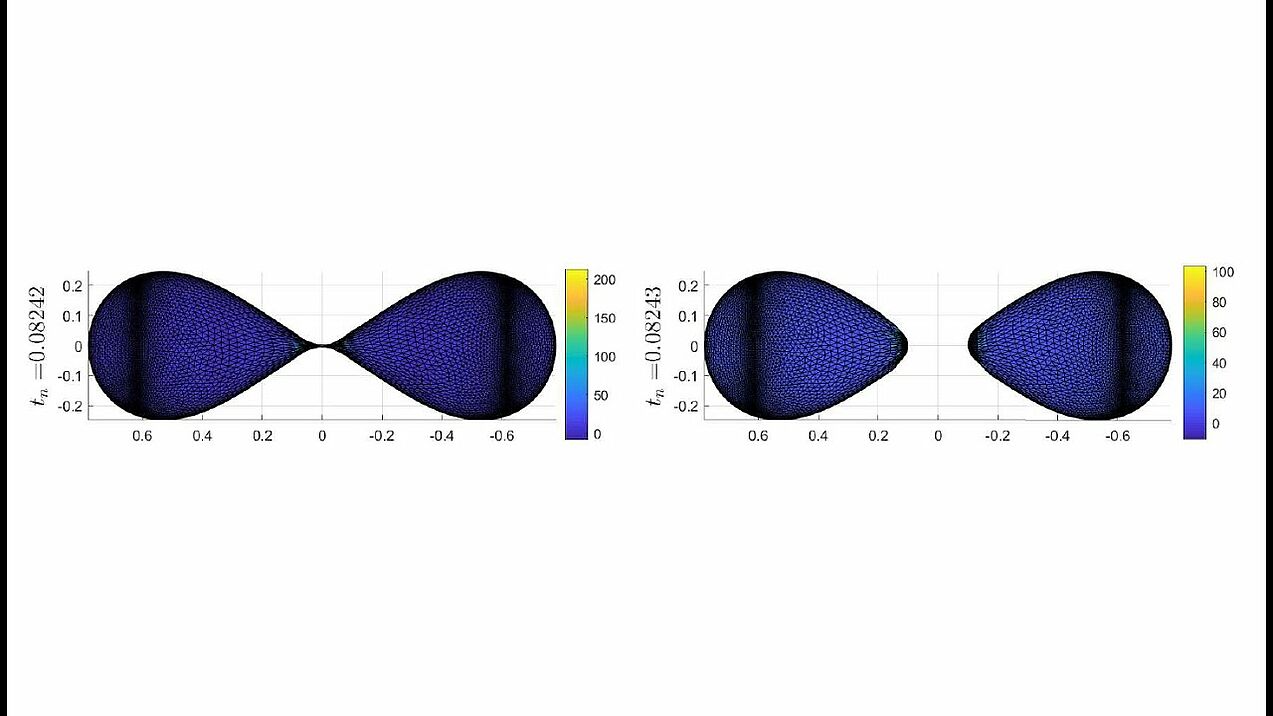
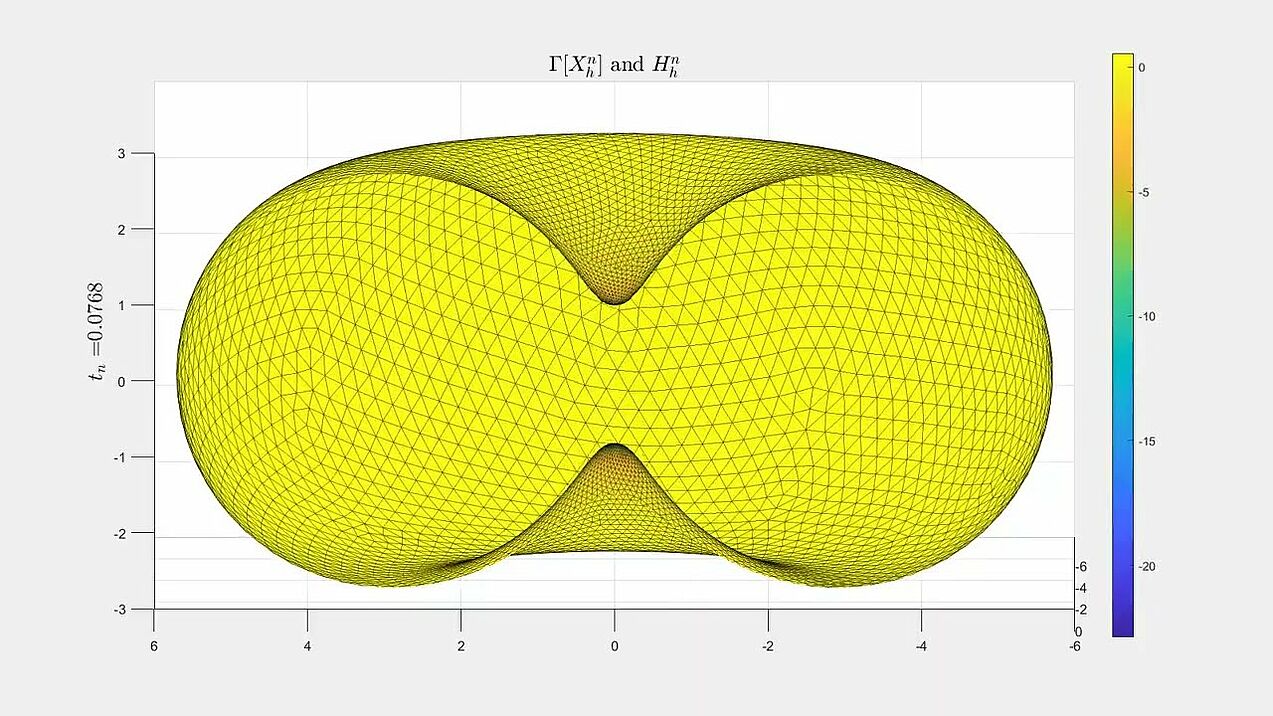
Numerical experiments for mean curvature flow algorithm from our paper.
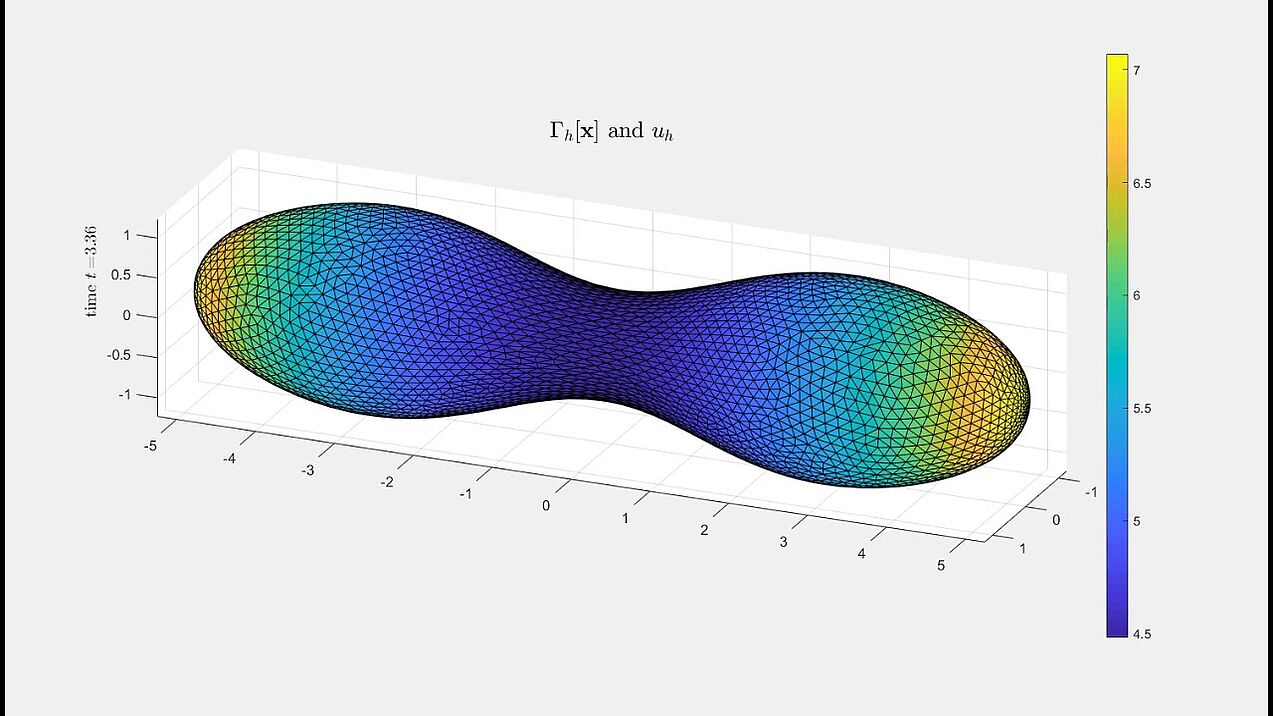
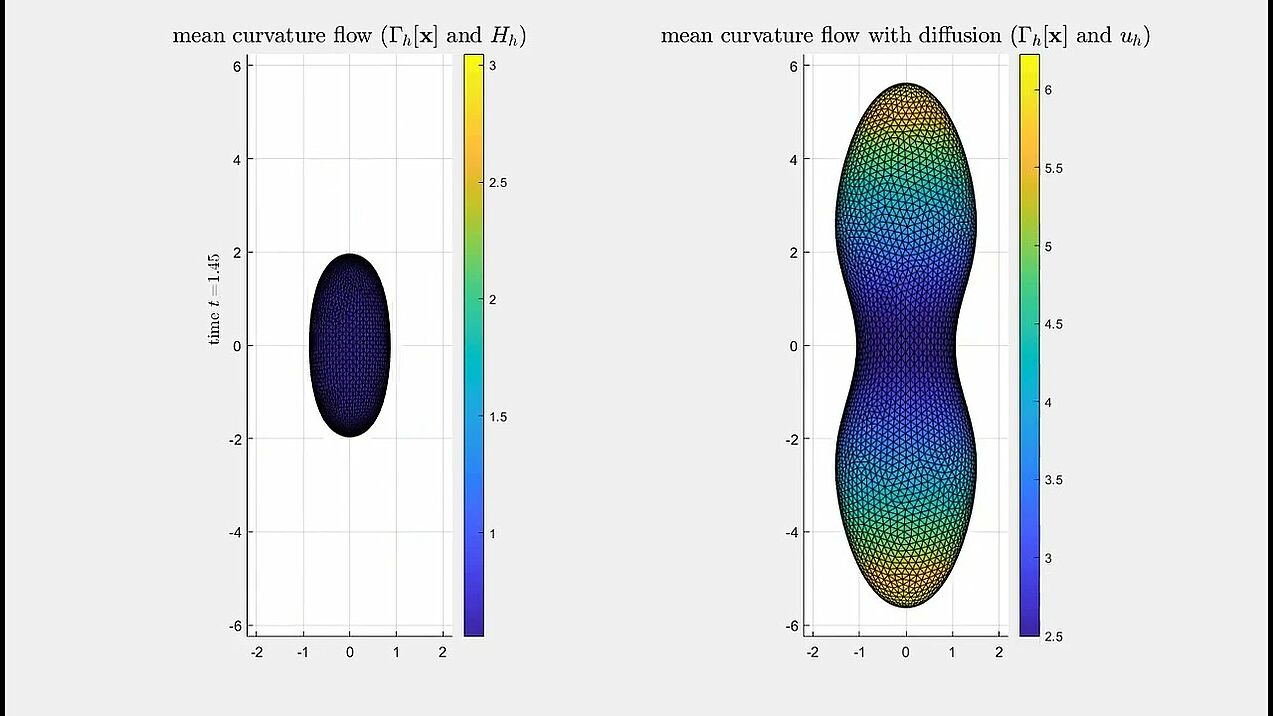
A dumbbell-shaped surface developing a pinch singularity along the flow (with a zoom-in on the singularity).
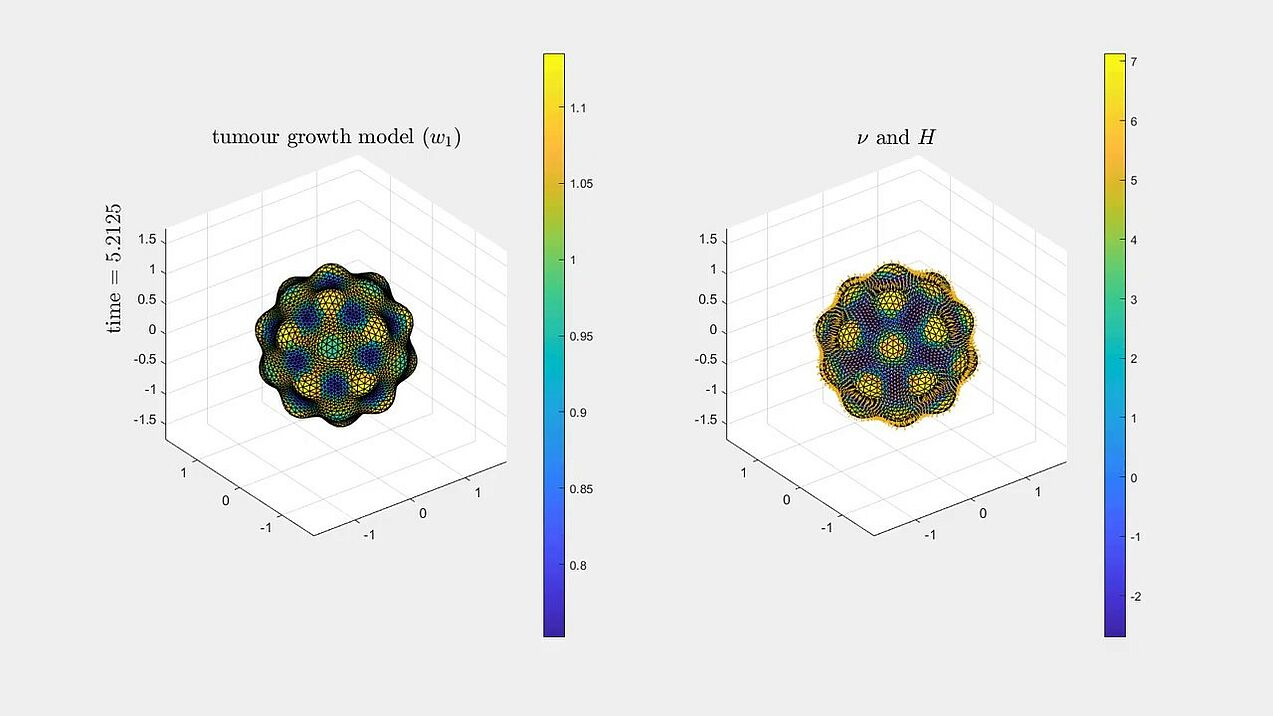
Forced mean curvature flow
Numerical experiments for a tumour growth model using the algorithm from the paper (with two different reaction parameters \gamma = 30 and 300):
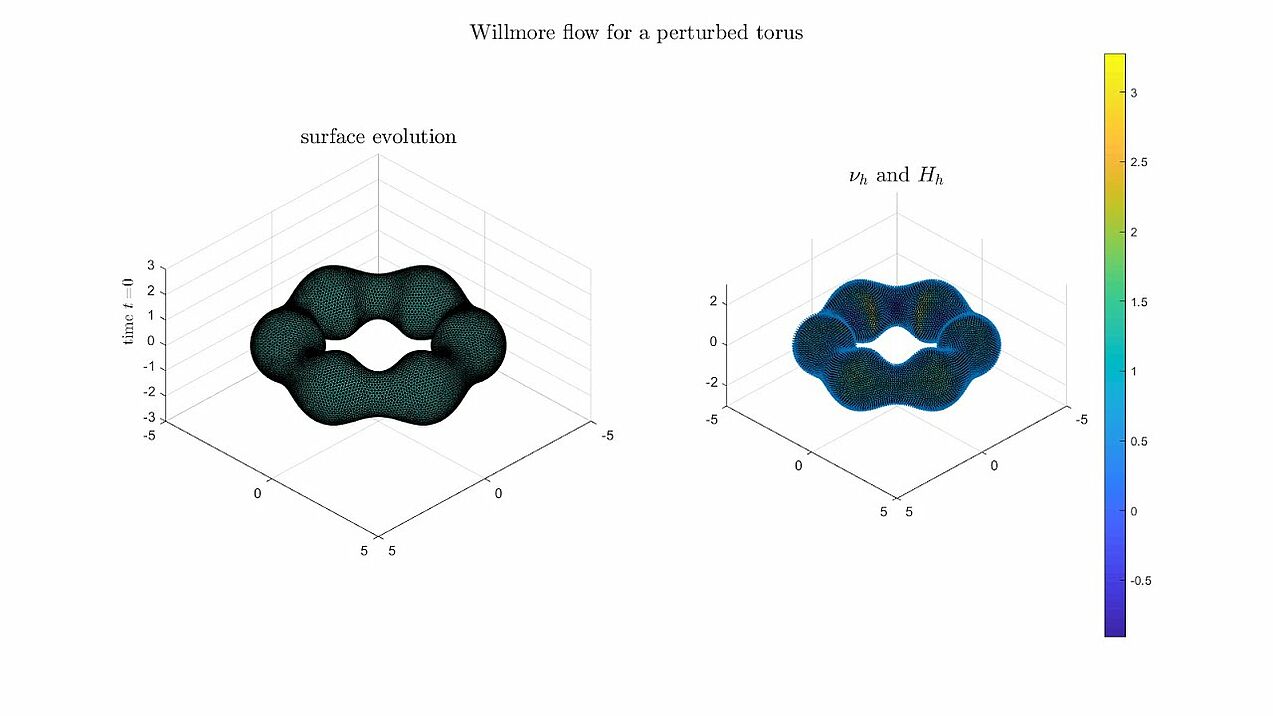
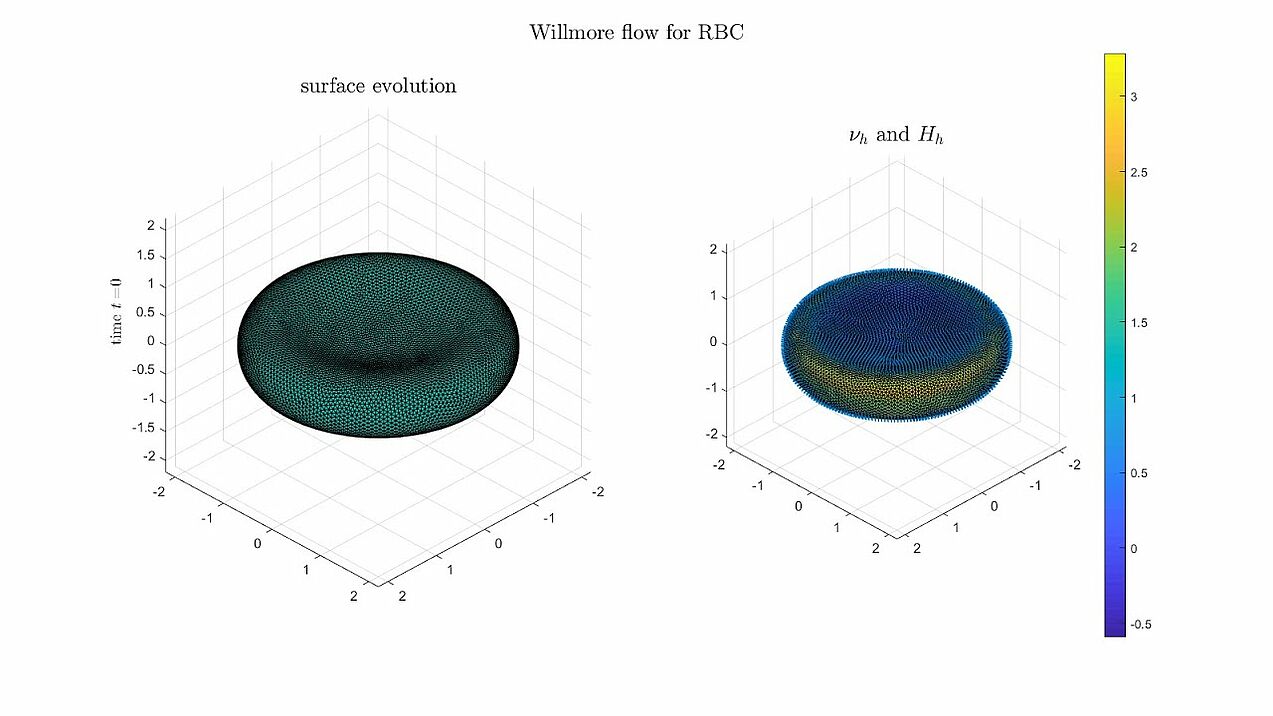
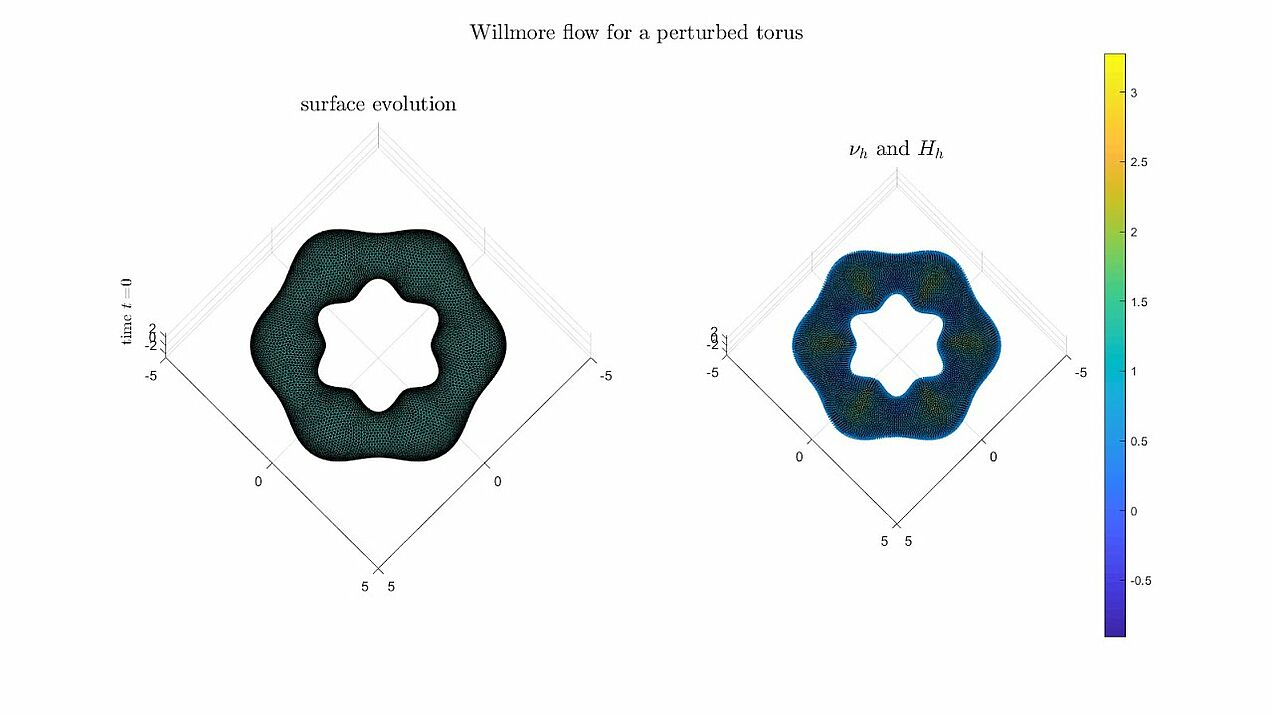
Willmore flow
Some numerical experiments for Willmore flow using the algorithm analysed in the paper.
- Topologically spherical objects are known to converge to a sphere, while minimising the Willmore energy (W(\Gamma) \to 8\pi).
- Surfaces of genus 1 are converging to a Clifford torus minimising the Willmore energy (W(\Gamma) \to 4\pi^2).
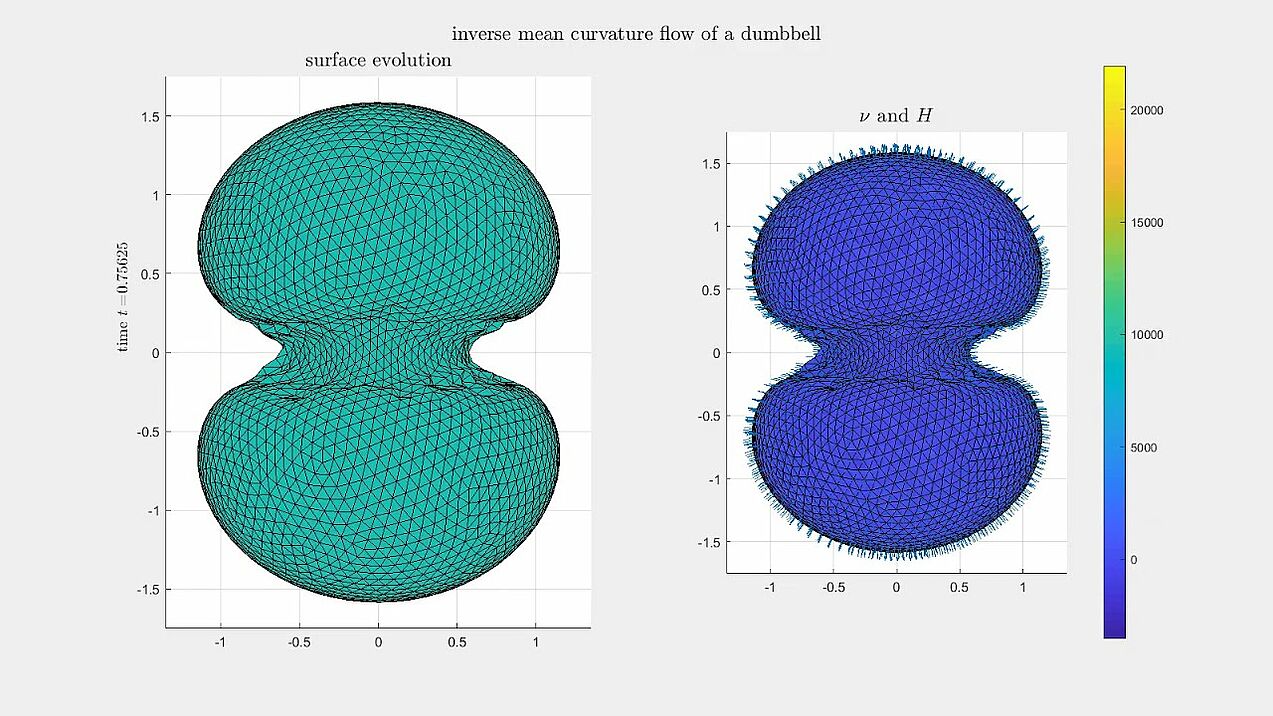
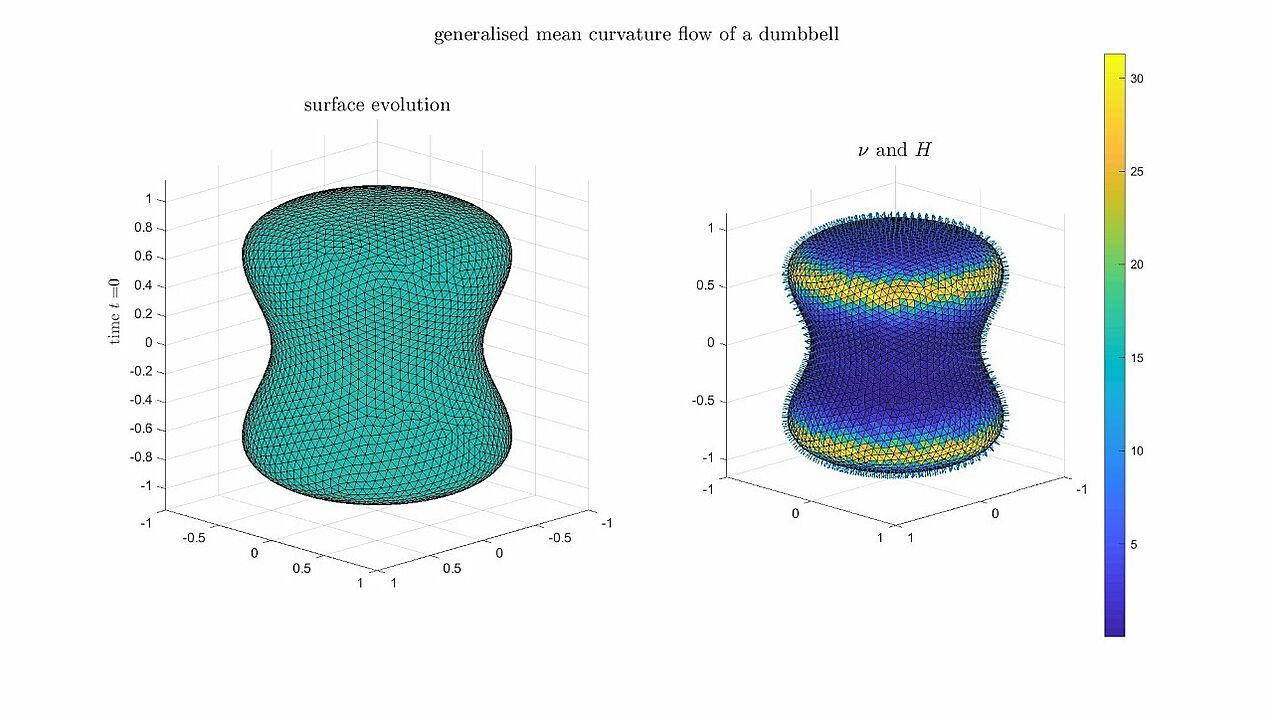
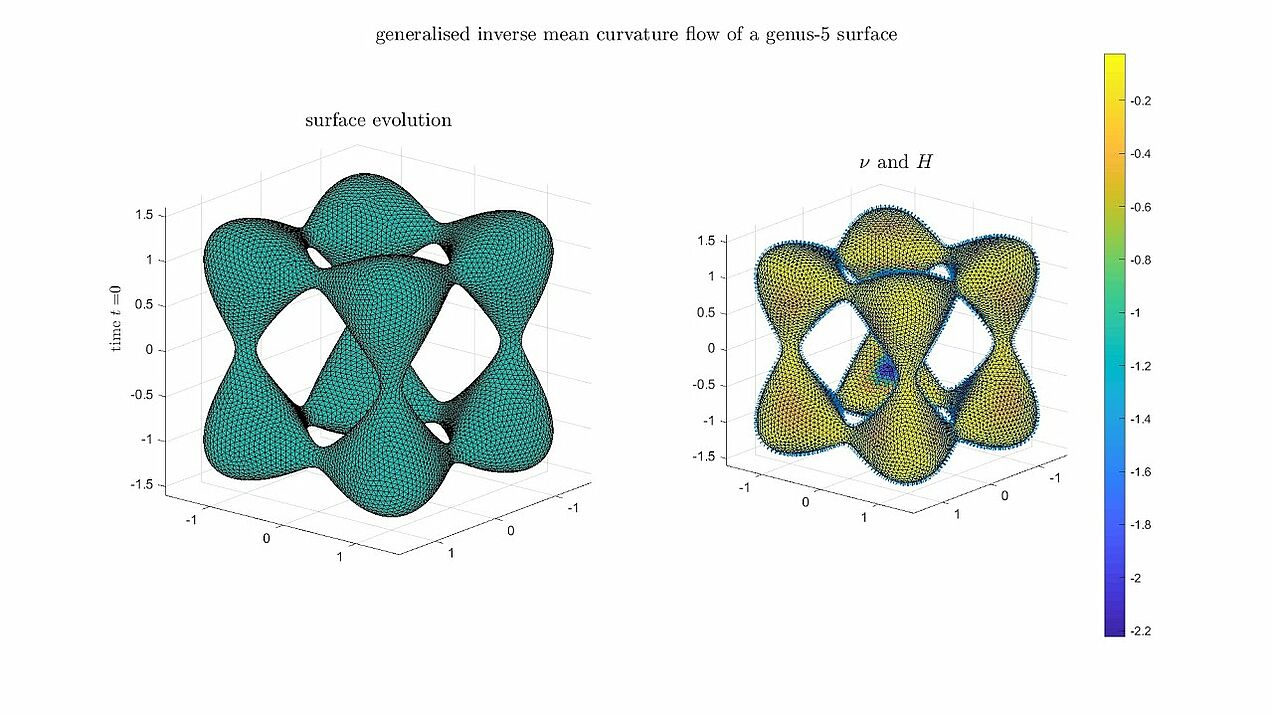
Generalised mean curvature flow
Numerical experiments for an algorithm for generalised mean curvature flows, i.e. the surface velocity is given by v = - V(H) \nu_\Gamma.
A non-convex dumbbell-shaped surface evolving towards a singularity along inverse mean curvature flow (V(H) = - 1 / H).
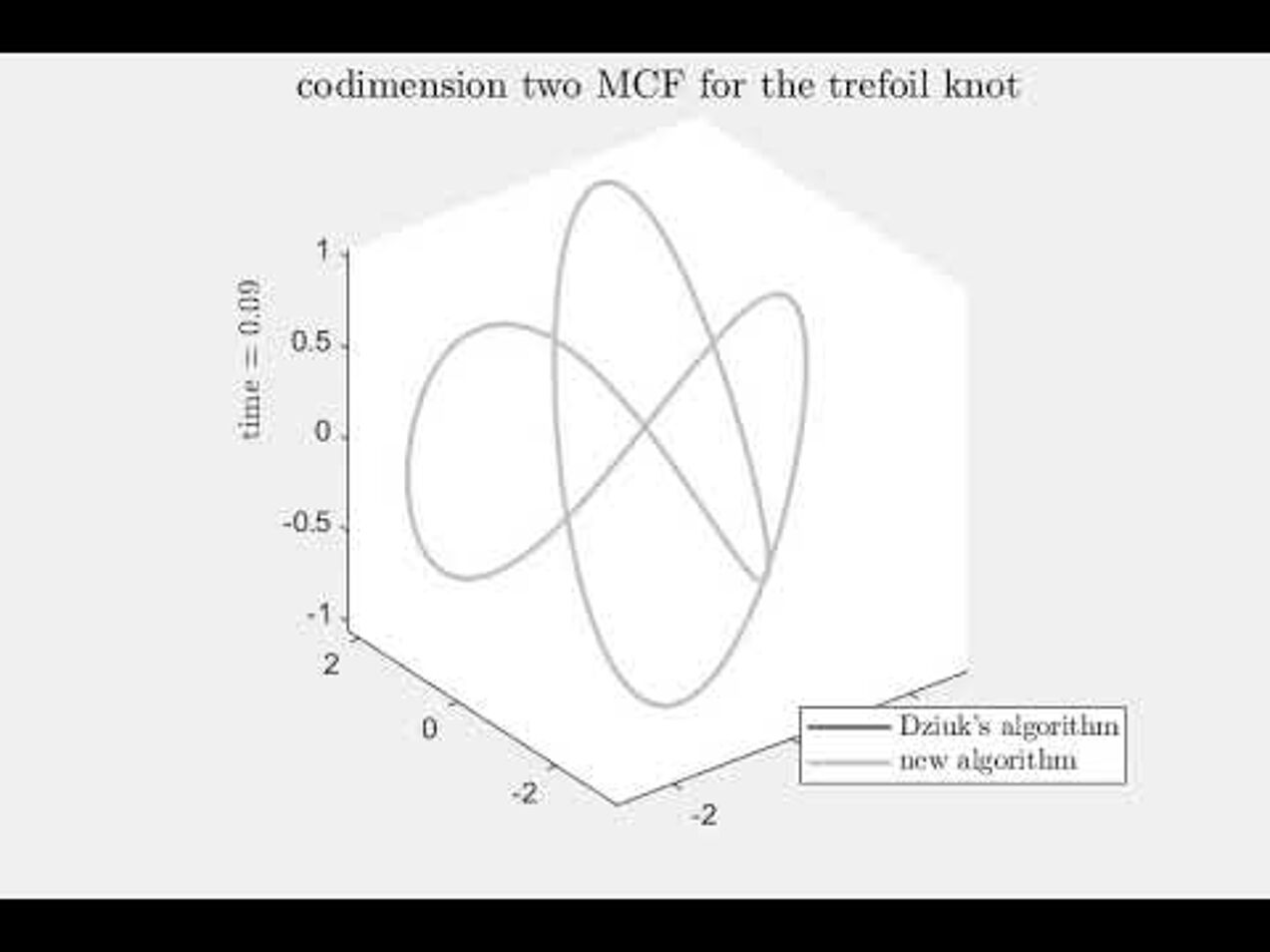
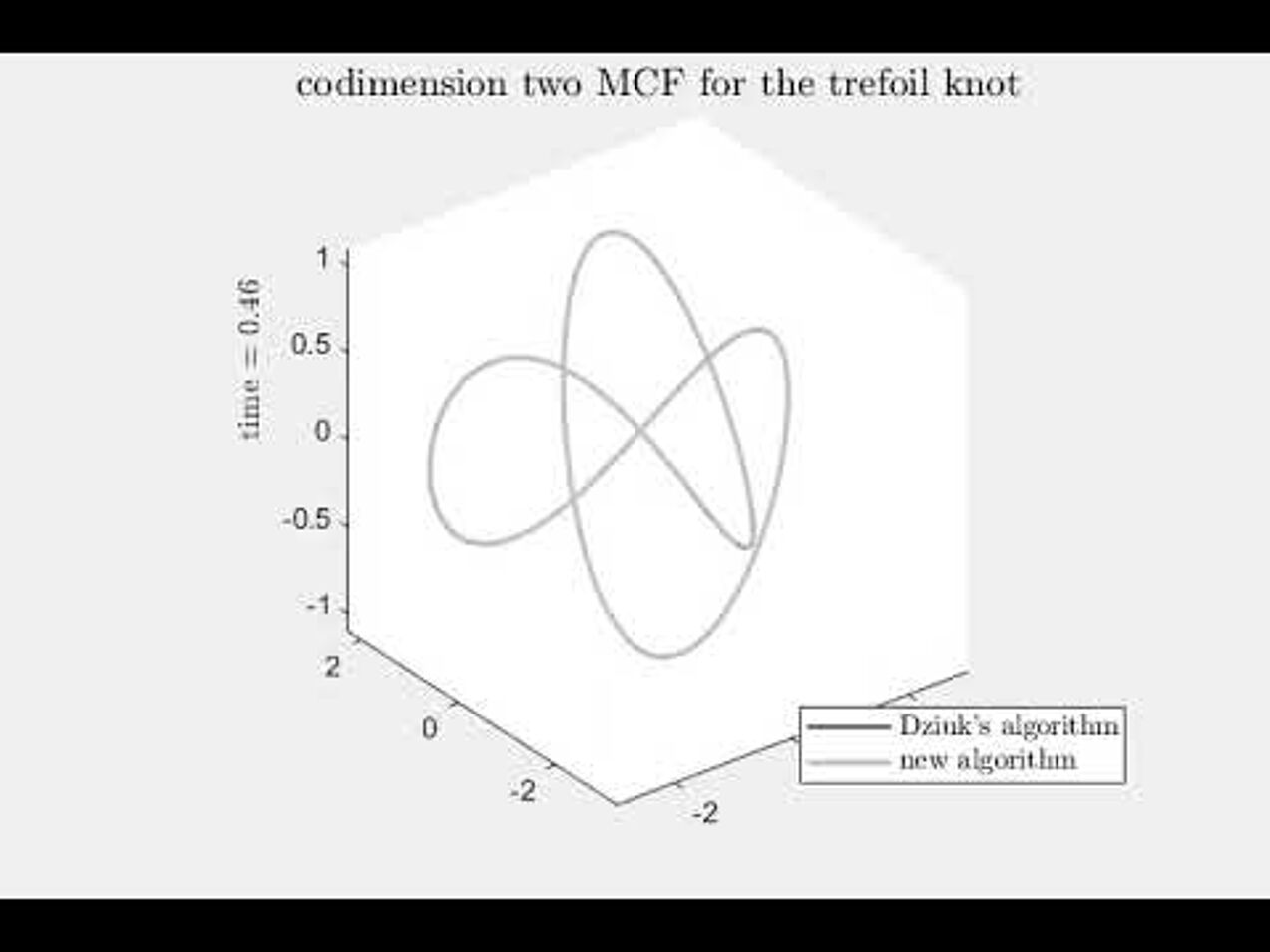
Mean curvature flow in higher codimension
Numerical experiments for an algorithm for mean curvature flow in codimension two.
A trefoil knot evolving under mean curvature flow in codimension 2.
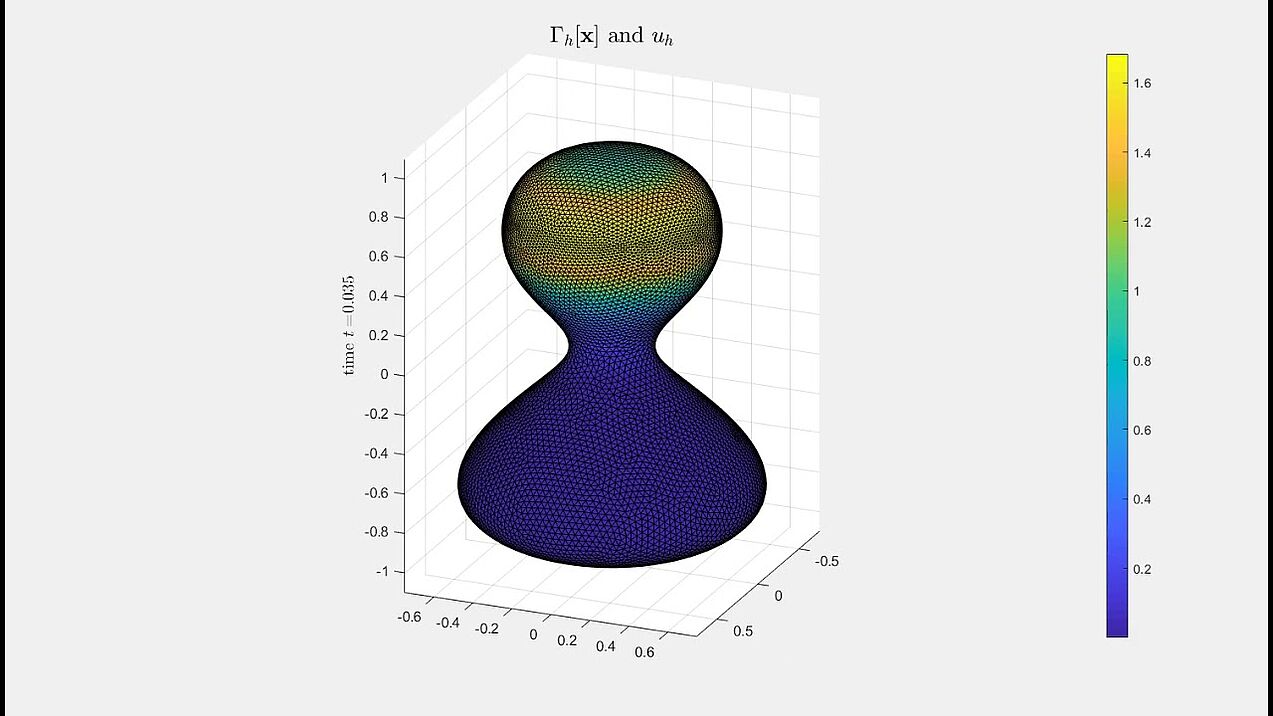
Mean curvature flow interacting with diffusion
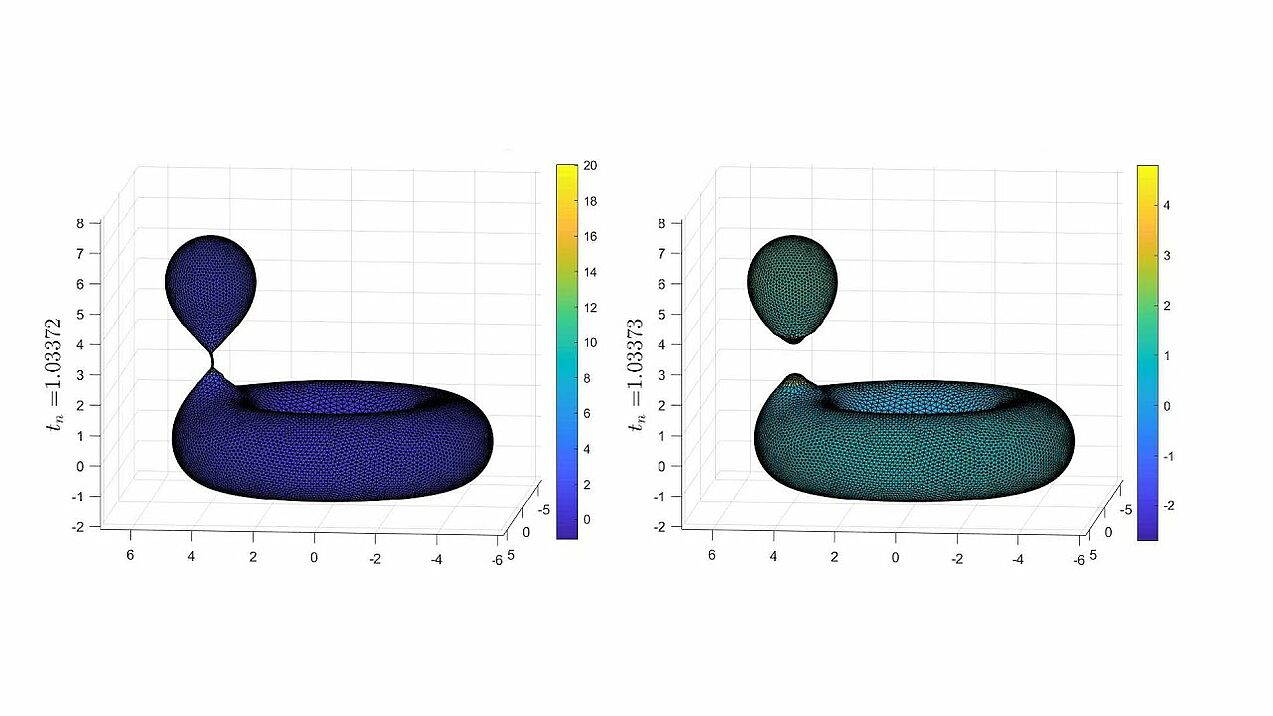
Numerical surgery for mean curvature flow
Inspired by surgery process of Huisken & Sinestrari and Brendle & Huisken, this paper proposes a numerical mean curvature flow algorithm with surgery for surfaces.
Resolving a pinch singularity of a dumbbell-shaped surface.
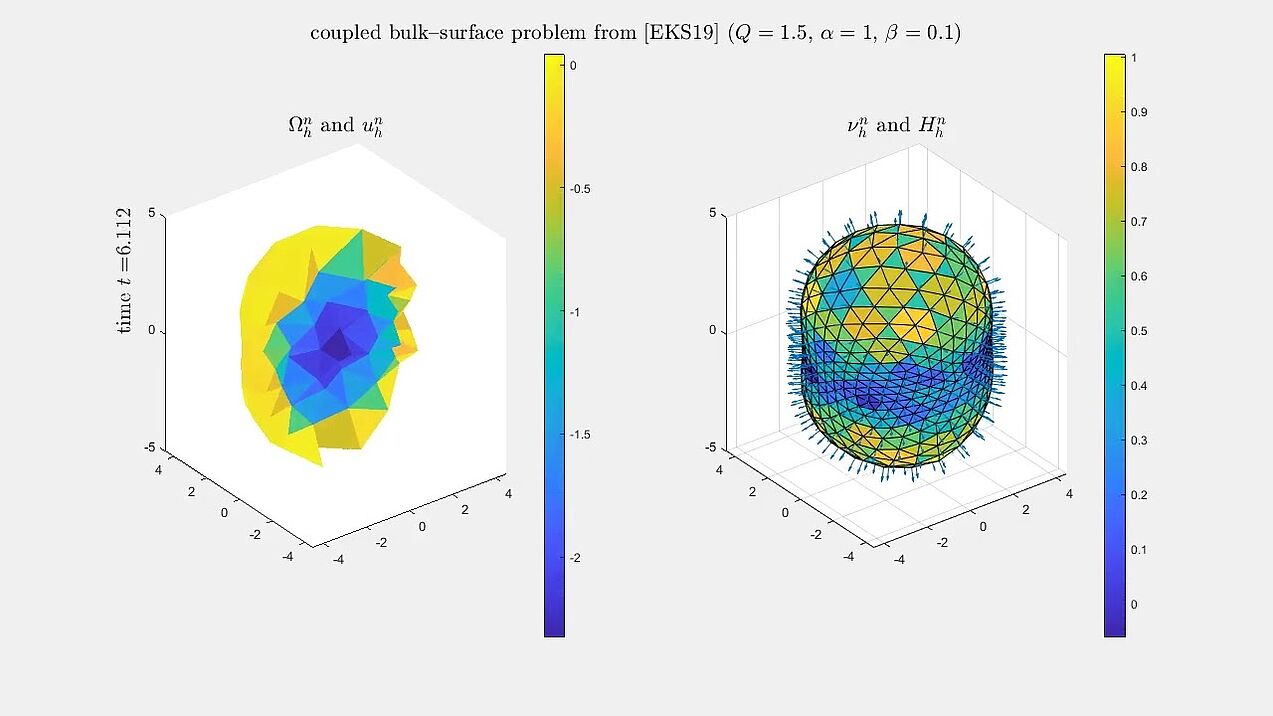
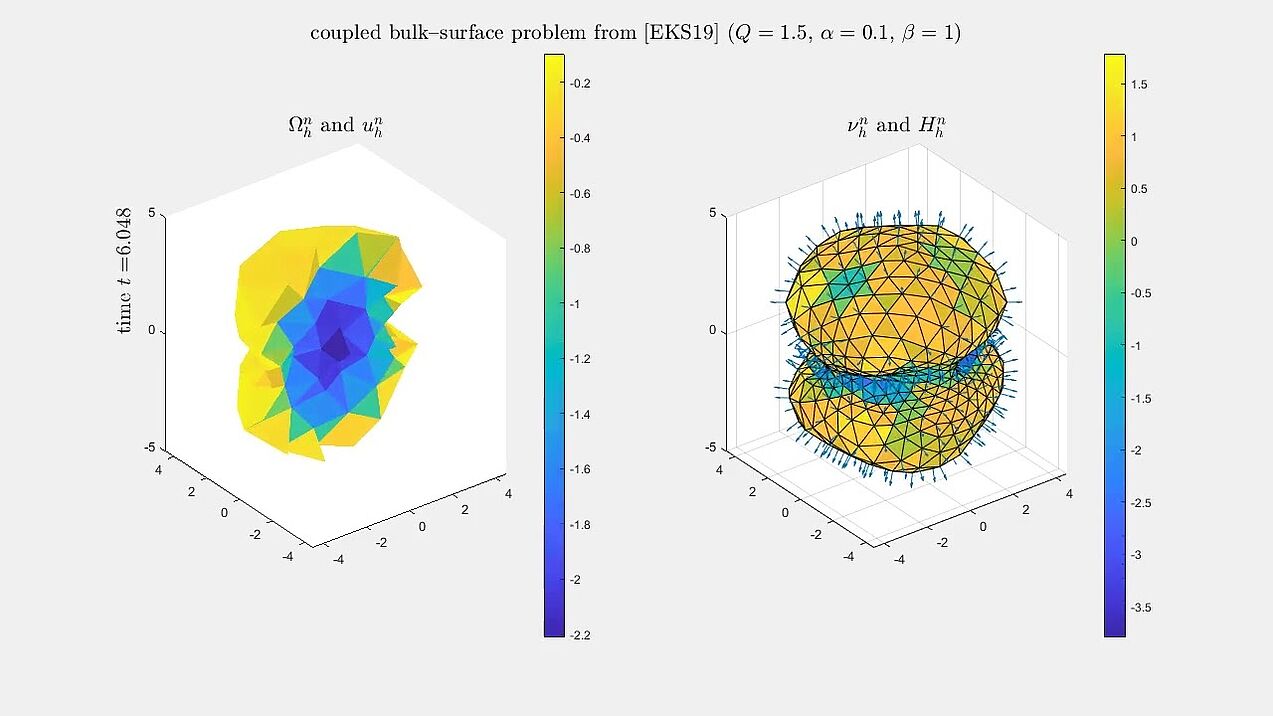
Bulk–surface model of tumour growth
Numerical simulations for an evolving bulk--surface finite element method for a model of tissue growth, which is a modification of the model of Eyles, King and Styles (2019).
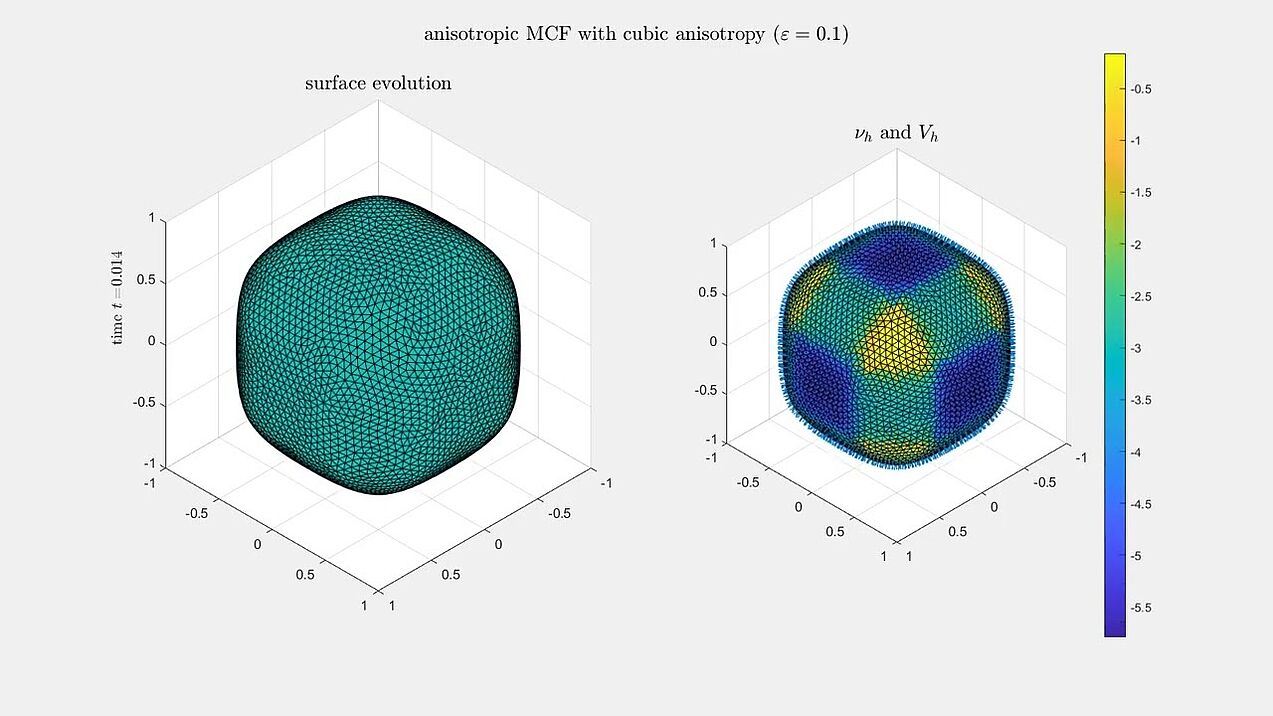
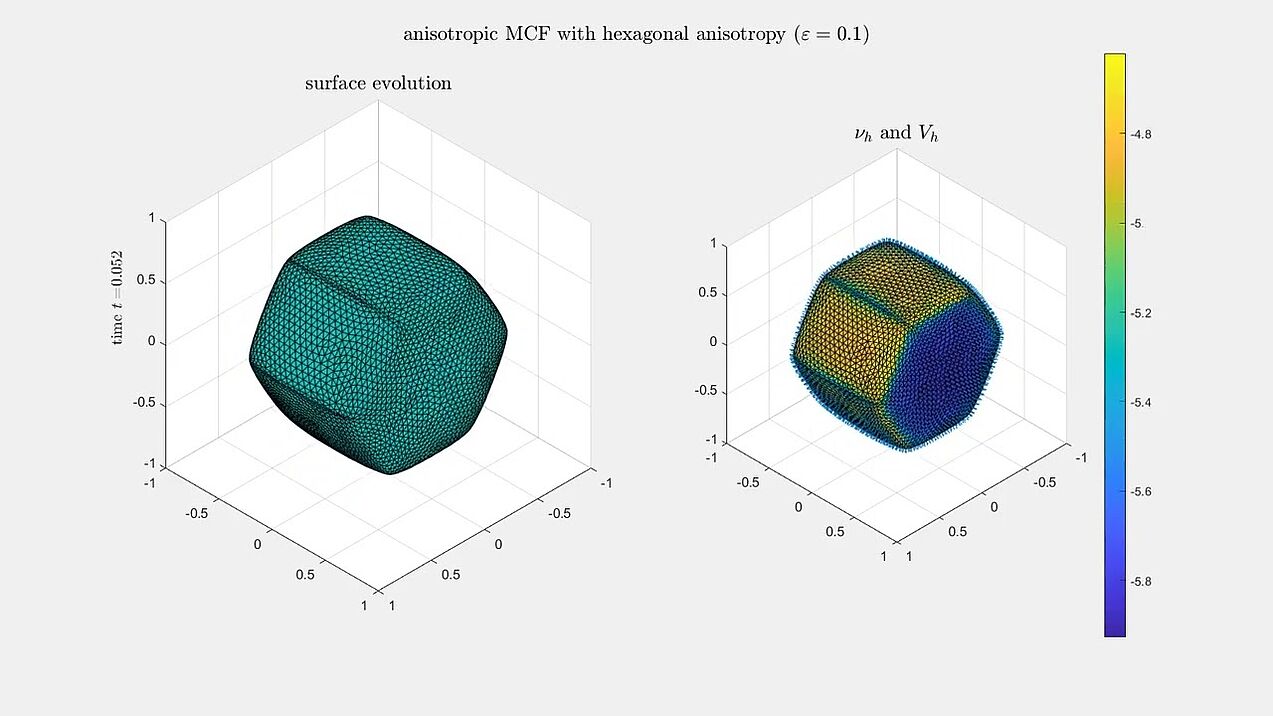
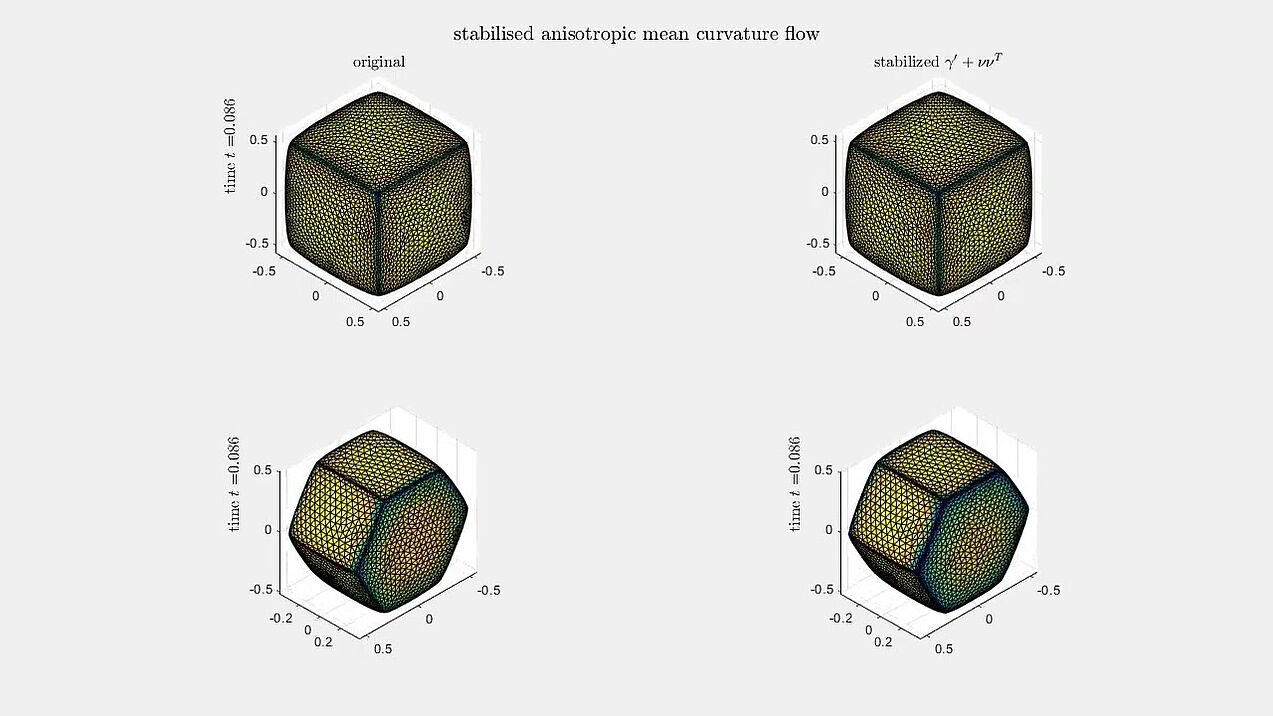
Anisotropic mean curvature flow
Numerical experiments for anisotropic mean curvature flow algorithm from our paper.
A sphere evolving under anisotropic mean curvature flow with a cubic and a hexagonal anisotropy.
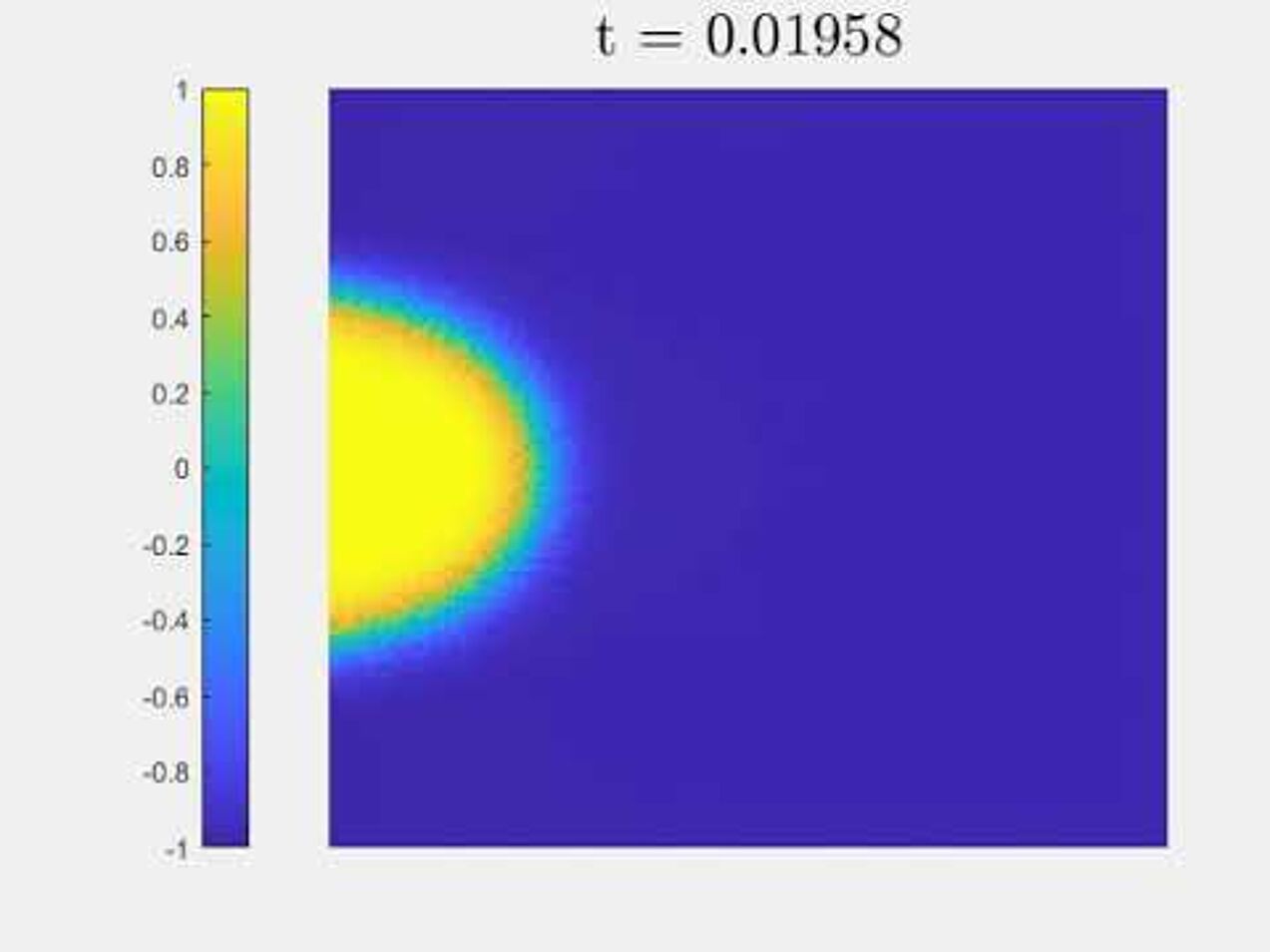
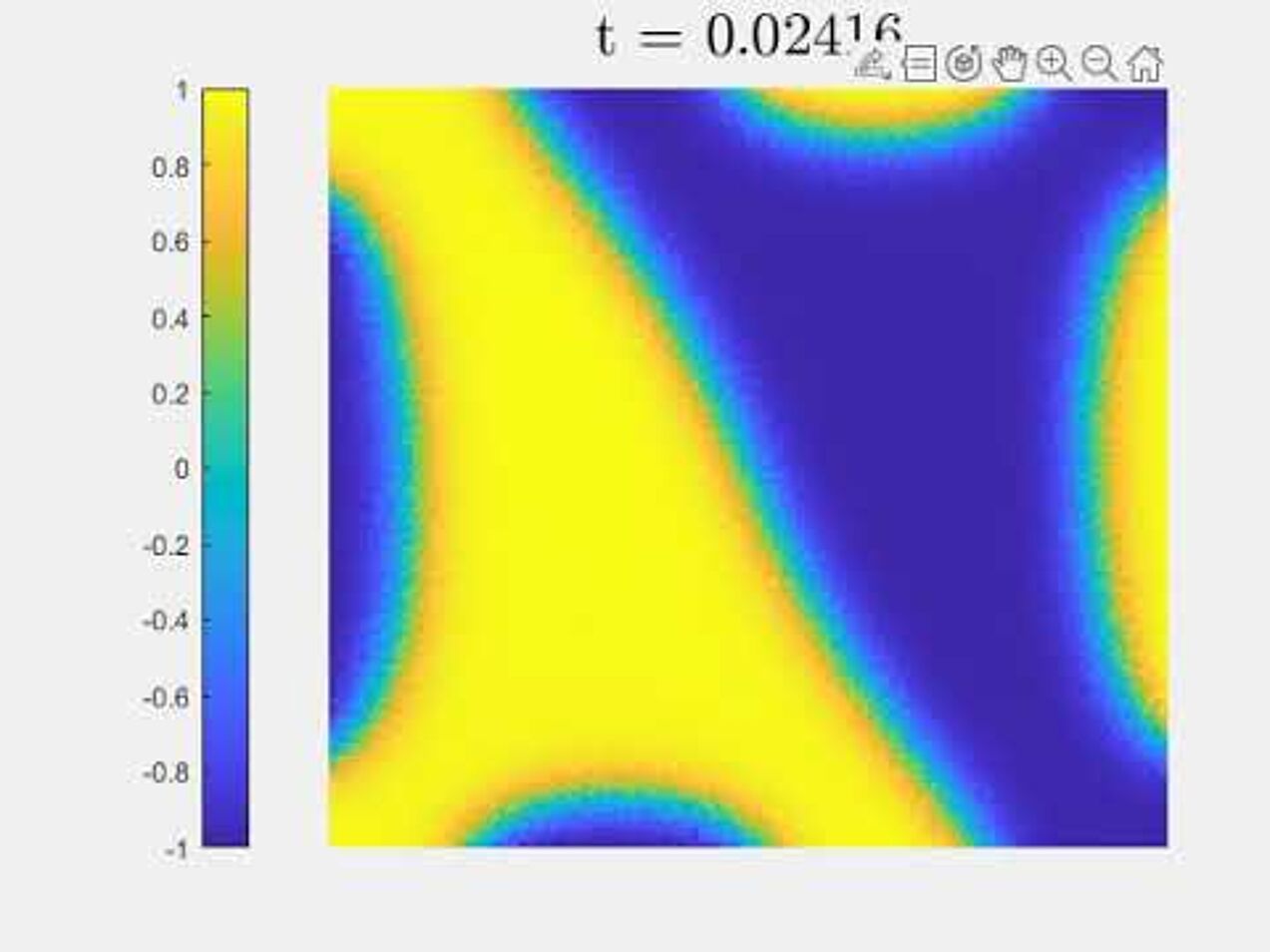
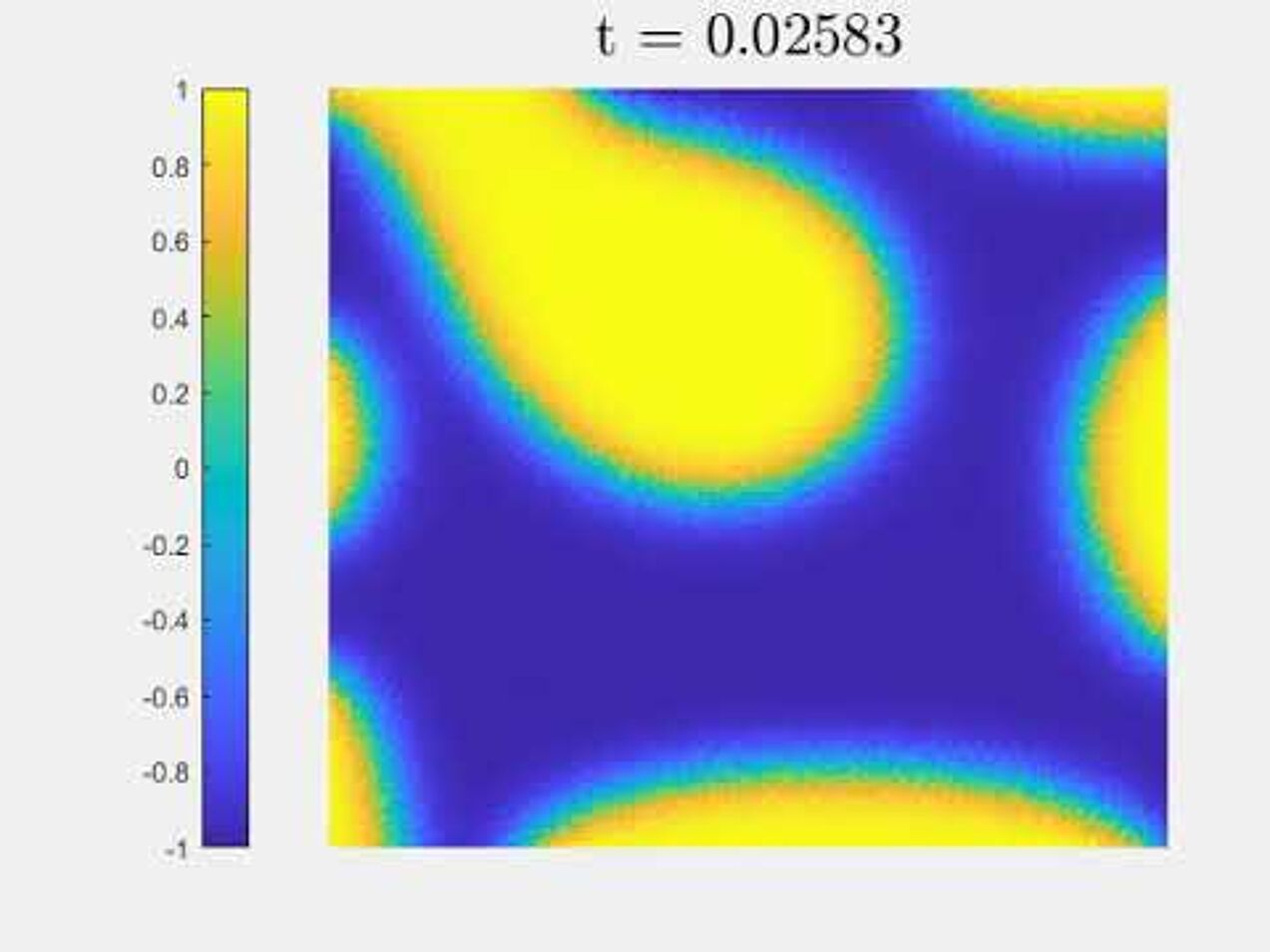
Cahn-Hilliard equation with dynamic boundary conditions
Numerical experiments for Cahn-Hilliard equation with dynmaic boundary conditions, with the algorithm from our paper.
An elliptically-shaped droplet evolving according to the GMS-model.
Bulk-surface Cahn-Hilliard system with dynamic boundary conditions
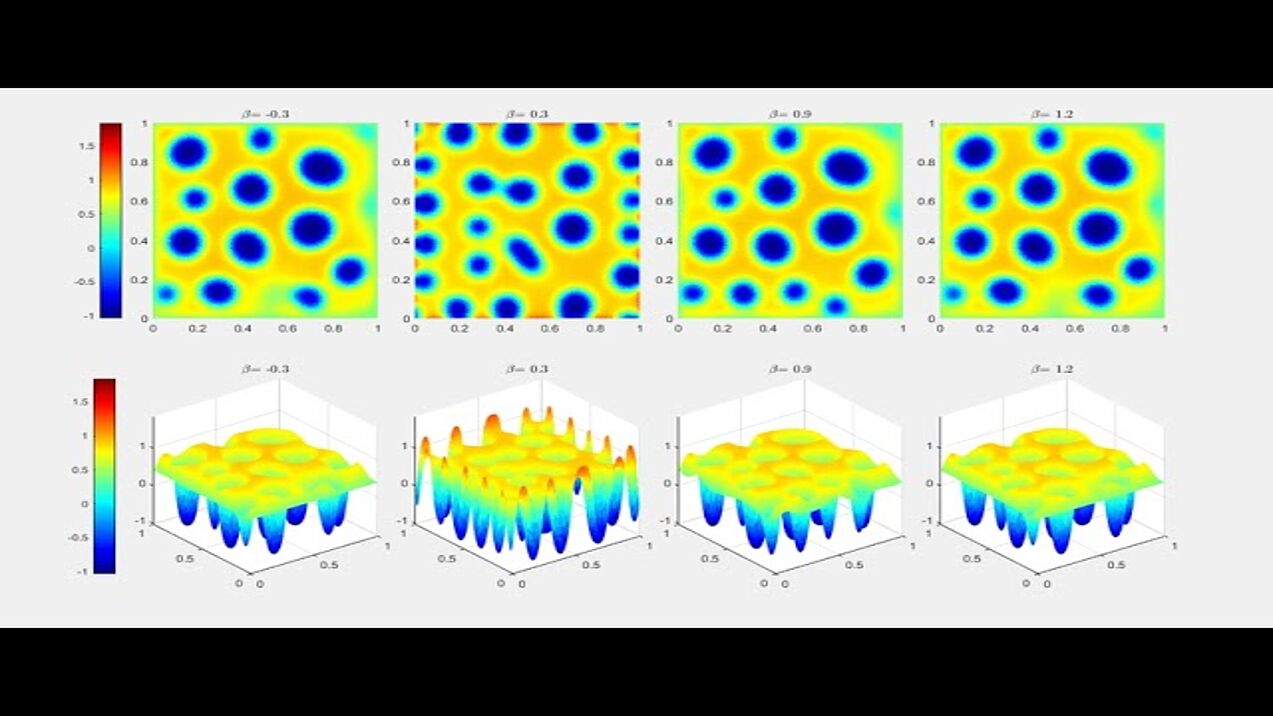
Numerical experiments for the bulk-surface Cahn-Hilliard system with general dynamic boundary conditions.
Evolution of a random initial data by the Cahn-Hilliard equation with transmission rate dependent dynamic boundary conditions with an affine linear transmission condition with constant parameter beta. Depending on the parameter beta we observe either Cahn-Hilliard phase-separation dynamics or near constant trace values.
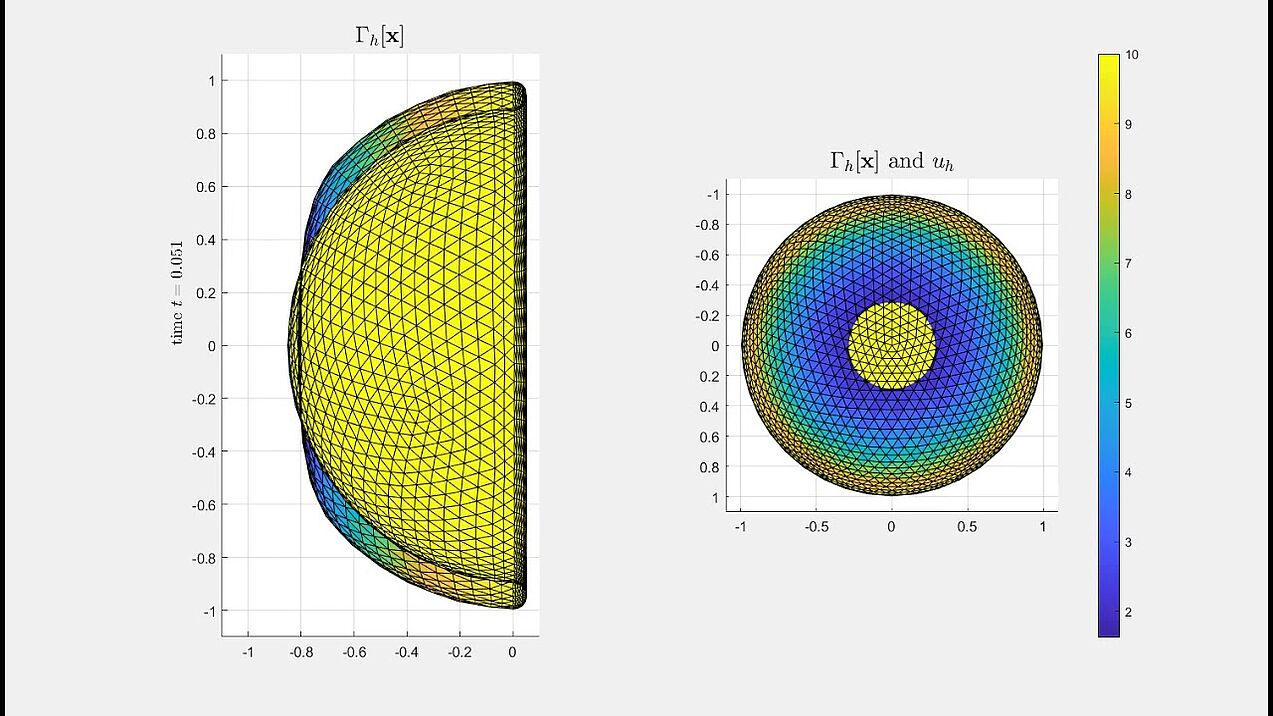
Adaptivity for parabolic PDEs on stationary surfaces
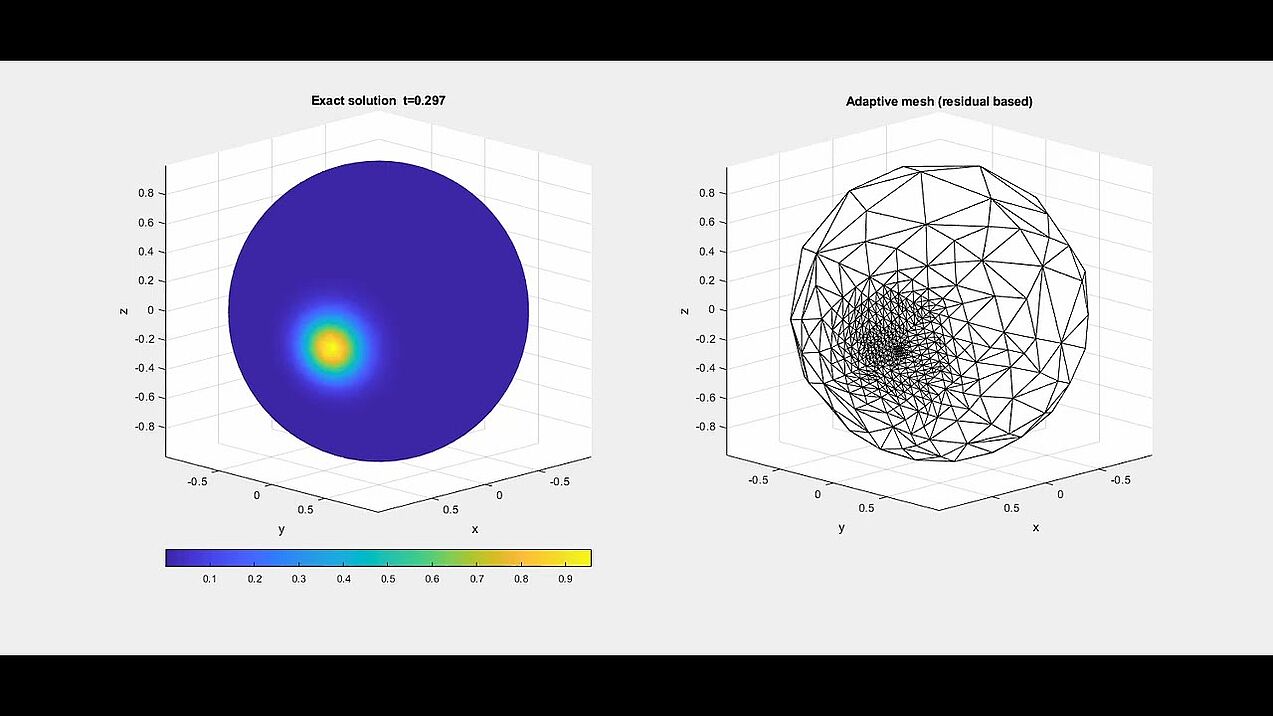
Numerical experiment of a residual based adaptive algorithm for parabolic PDEs on stationary surfaces.
We constructed an exact solution based on solving the parabolic heat equation on surfaces. This exact solution, a moving heat peak travelling along the equator while briefly vanishing for t=0.5, is presented on the left. The adaptive mesh for solving for the numerical solution, based on the residual based a posteriori error analysis, is given on the right.