Geometric flows and surface PDEs

Mean curvature flow (MCF)	Forced mean curvature flow	Willmore flow
Generalised mean curvature flow	MCF in in higher codimension	MCF–diffusion
Numerical surgery for MCF	Bulk–surface model of tumour growth	Anisotropic MCF

PDEs with dynamic boundary conditions

Cahn-Hilliard equation with dynamic boundary conditions
Bulk-surface Cahn-Hilliard system with dynamic boundary conditions

Adaptivity for surface PDEs

Adaptivity for parabolic PDEs on stationary surfaces

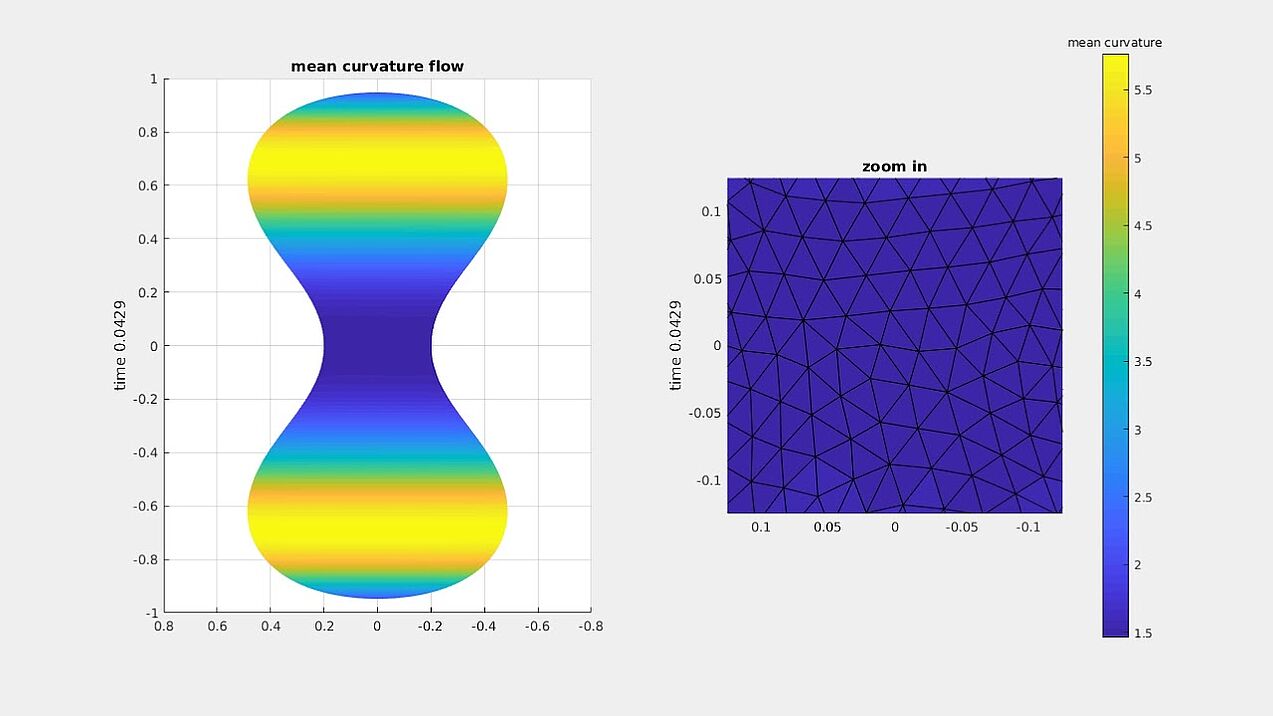
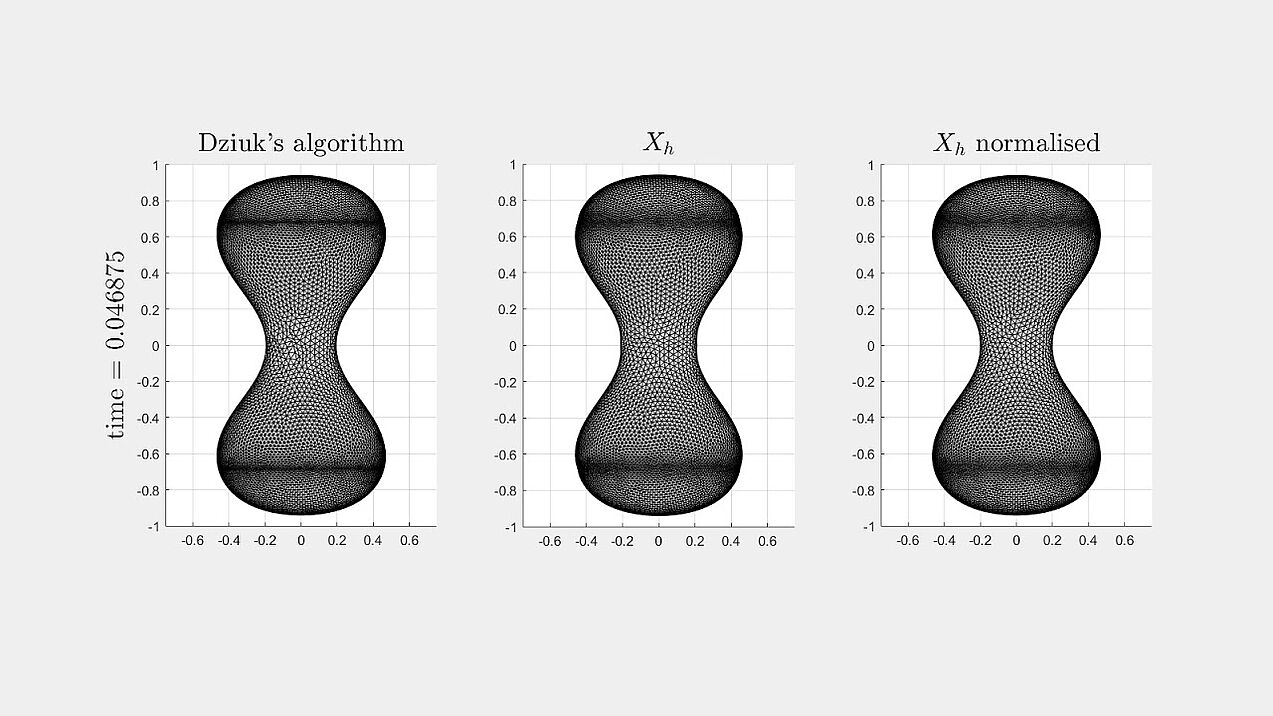
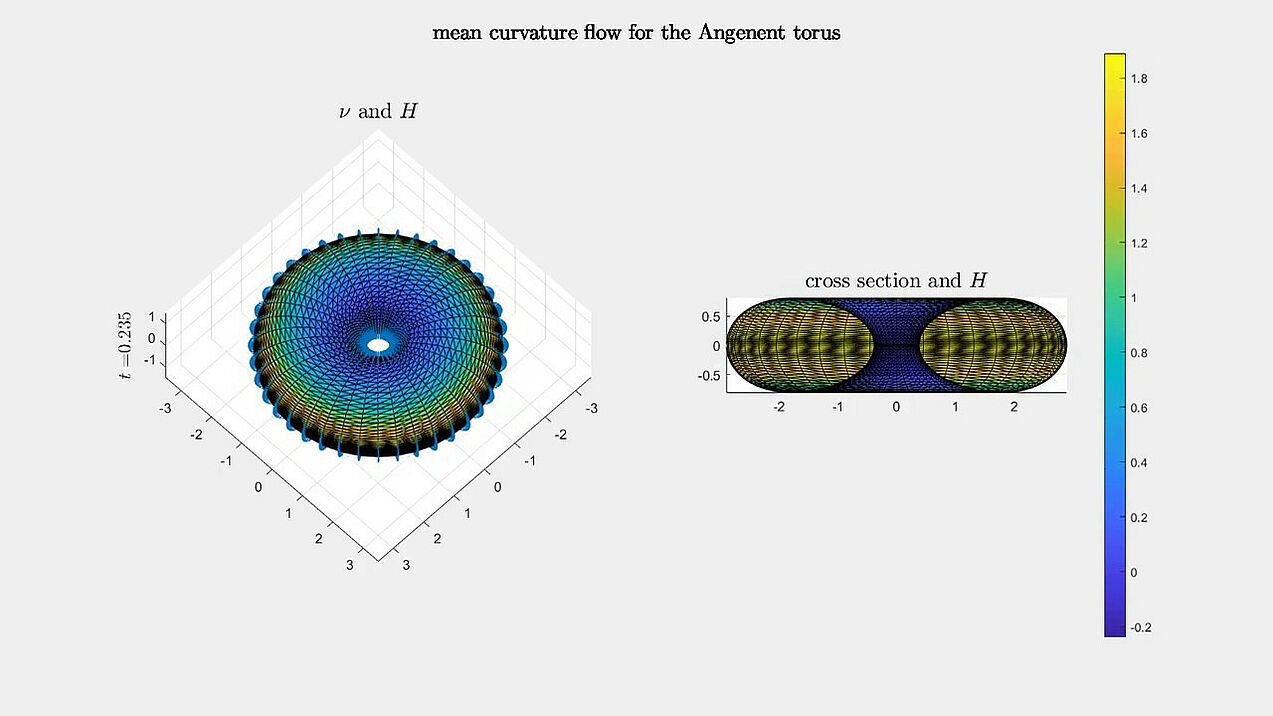
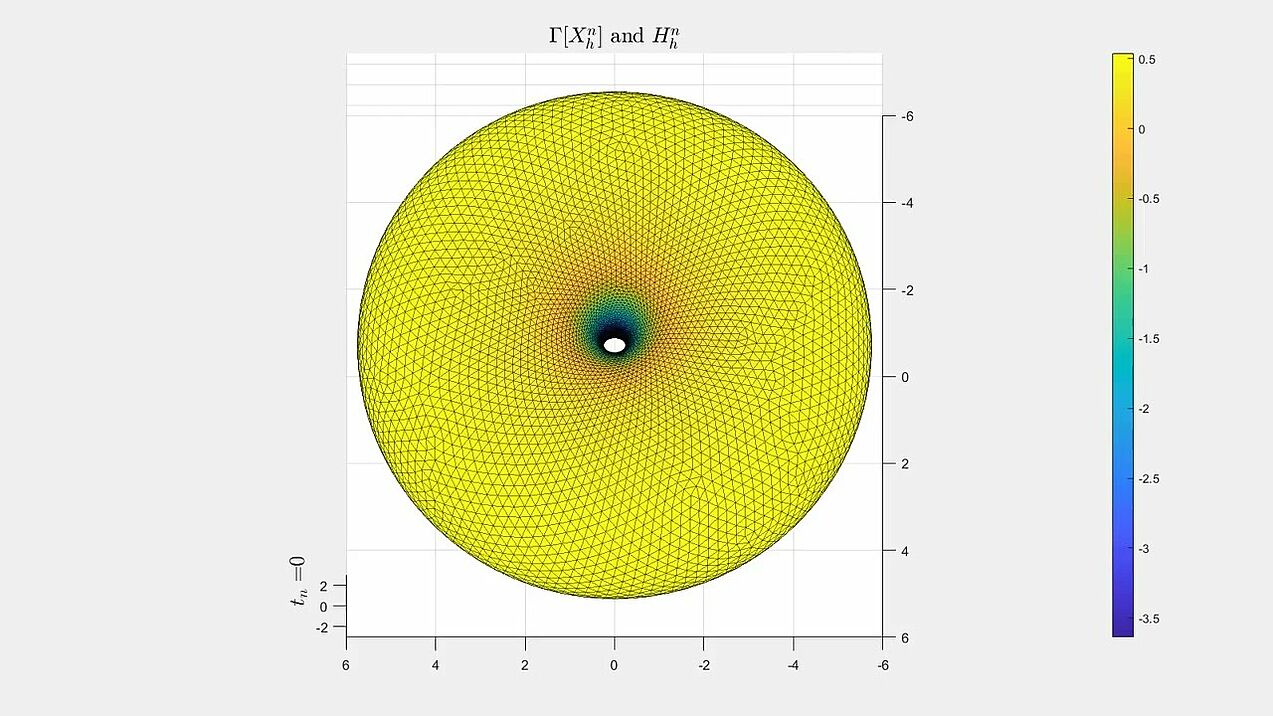
Mean curvature flow

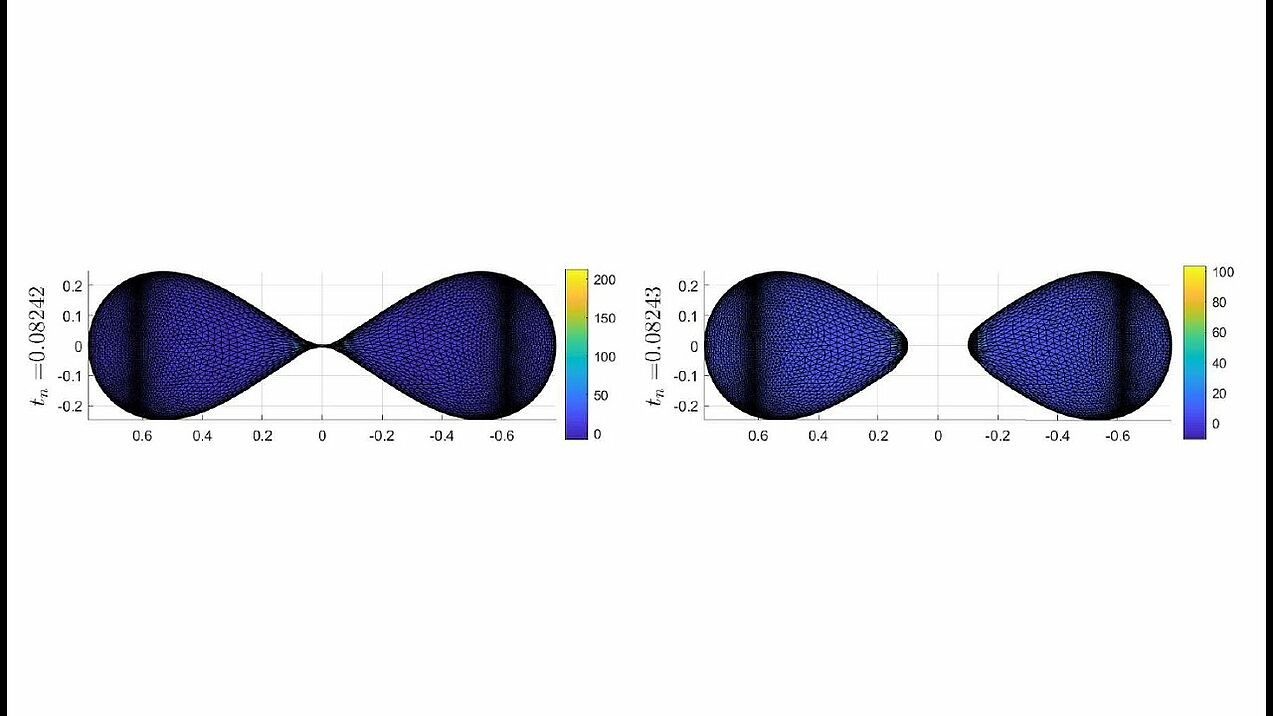
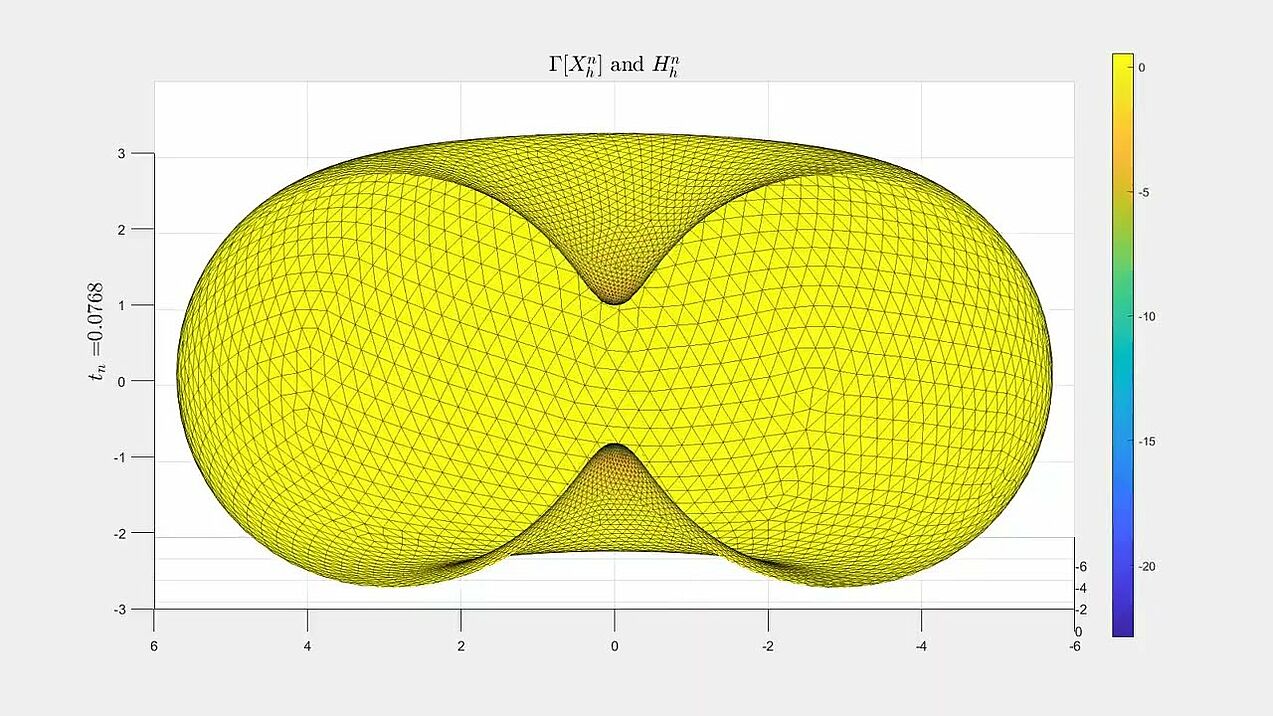
Numerical experiments for mean curvature flow algorithm from our paper.

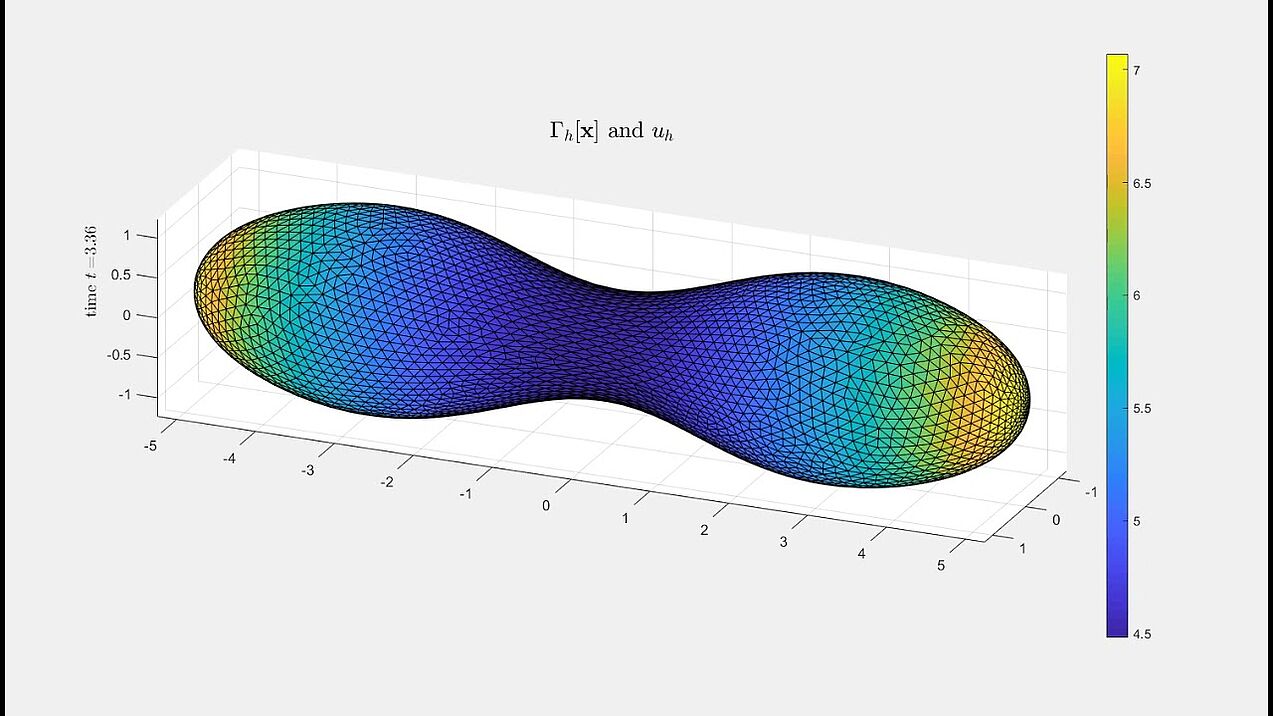
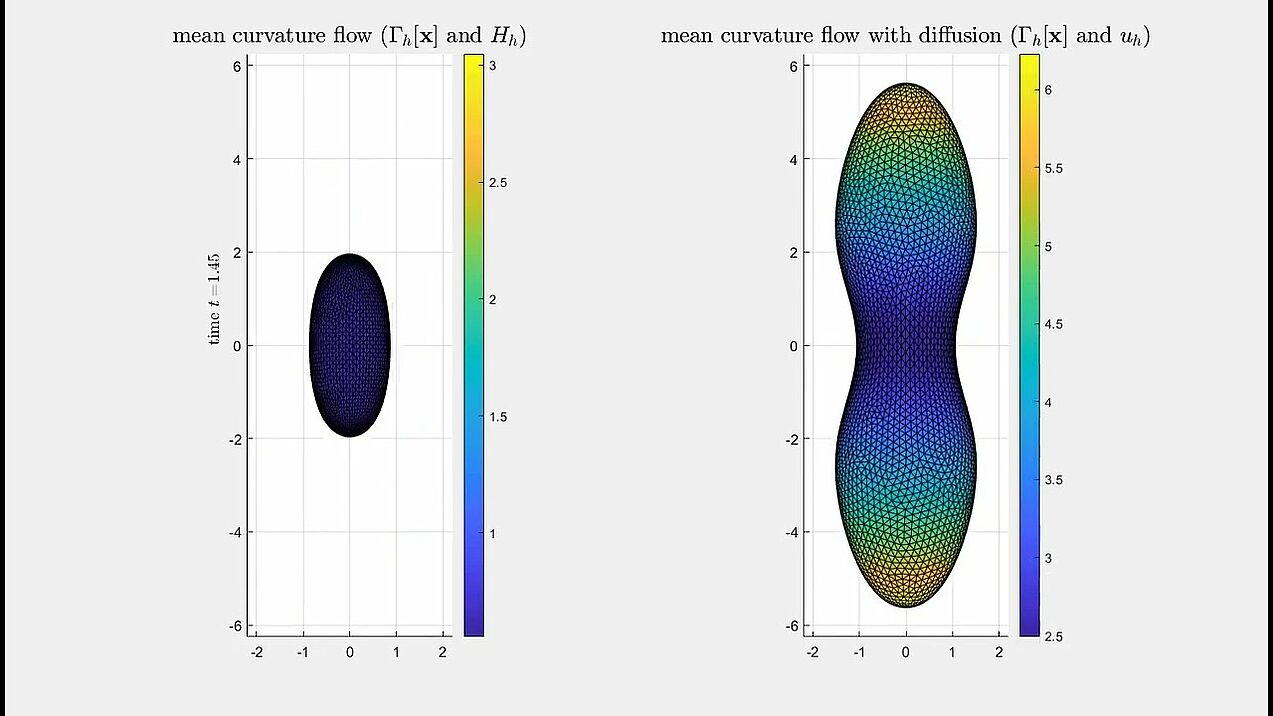
A dumbbell-shaped surface developing a pinch singularity along the flow (with a zoom-in on the singularity).

Comparison of algorithms for mean curvature flow

Comparing mean curvature flow algorithms

A self-similar solution to mean curvature flow — Angenent's doughnut

Self-similar mean curvature flow for the Angenent torus

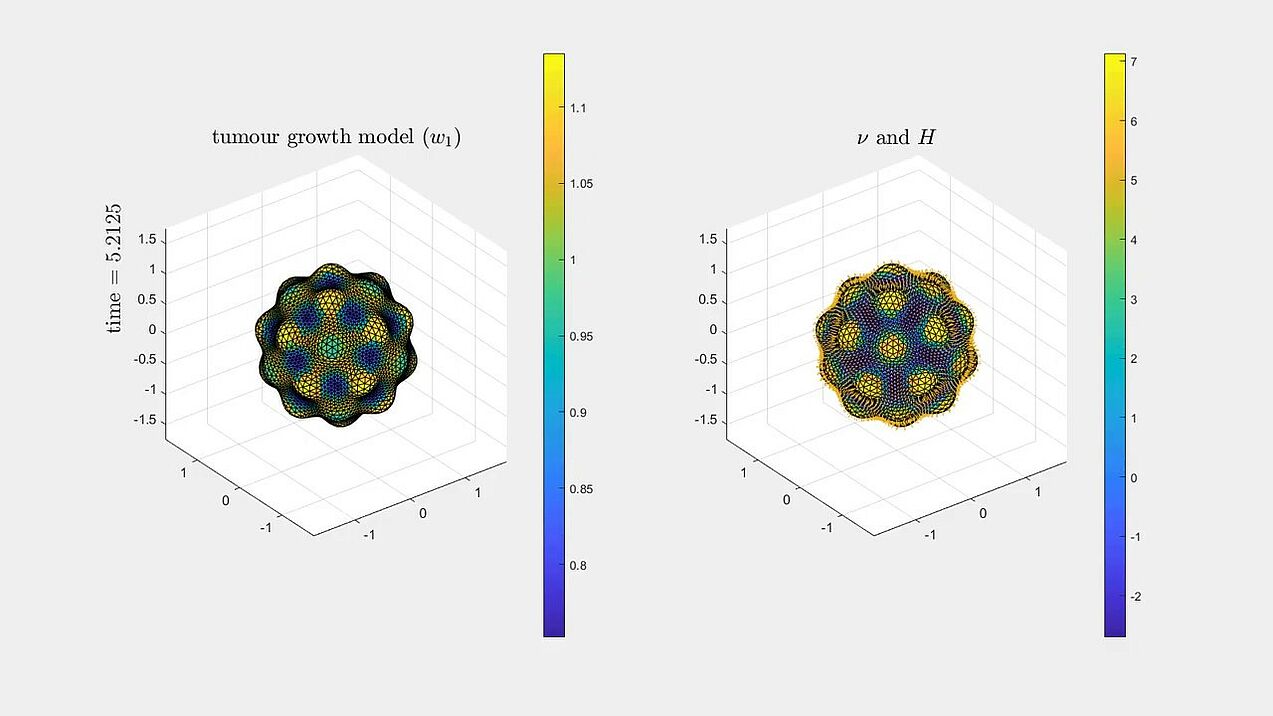
Forced mean curvature flow

Numerical experiments for a tumour growth model using the algorithm from the paper (with two different reaction parameters \gamma = 30 and 300):

Forced mean curvature flow modeling tumour growth (\gamma = 30)

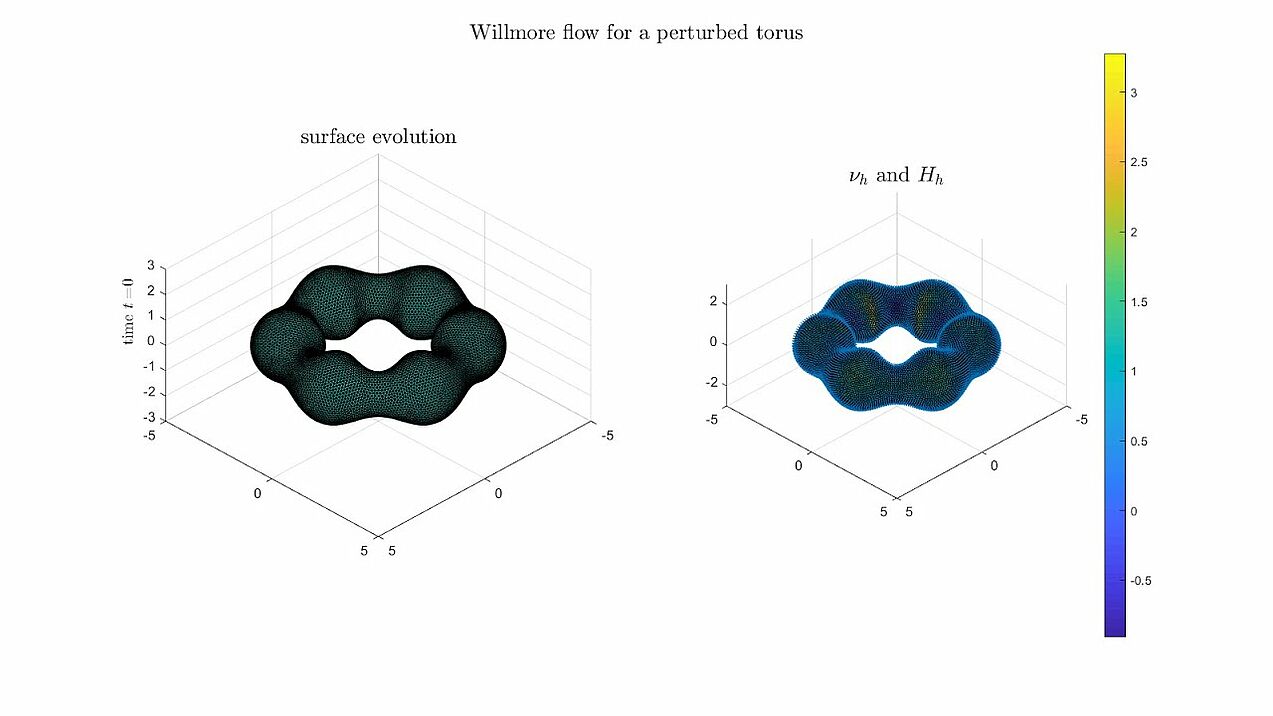
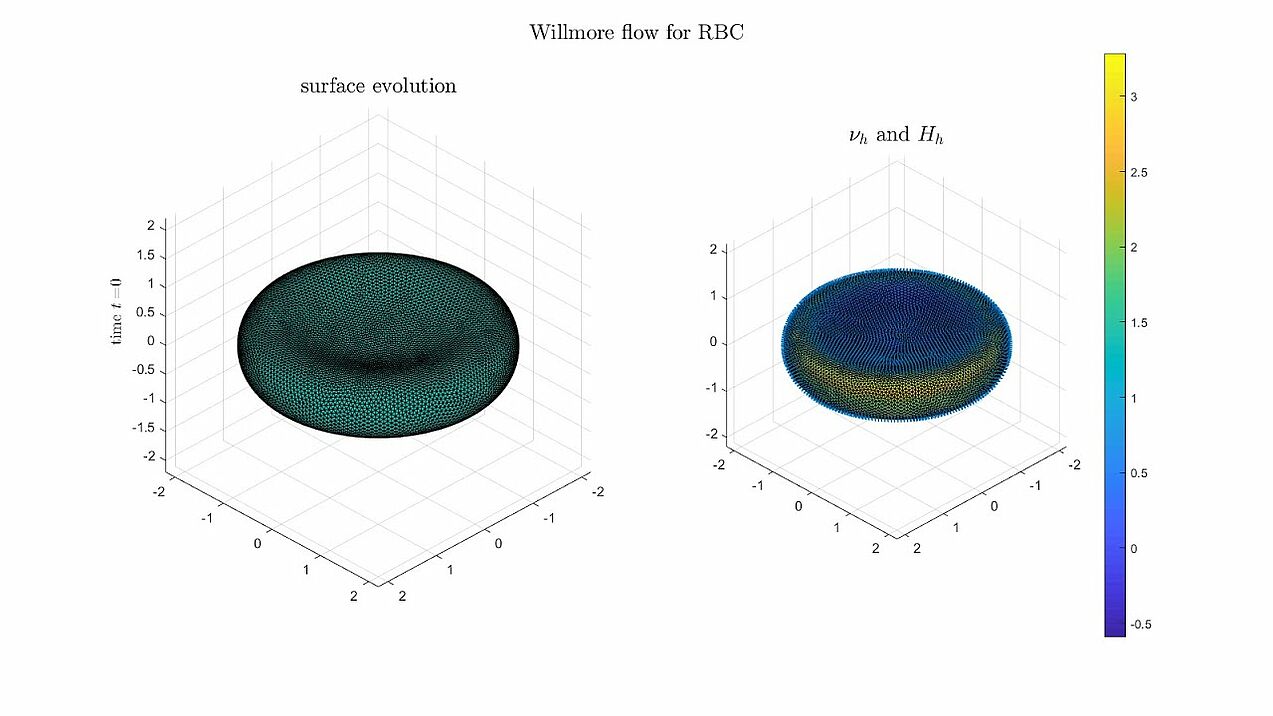
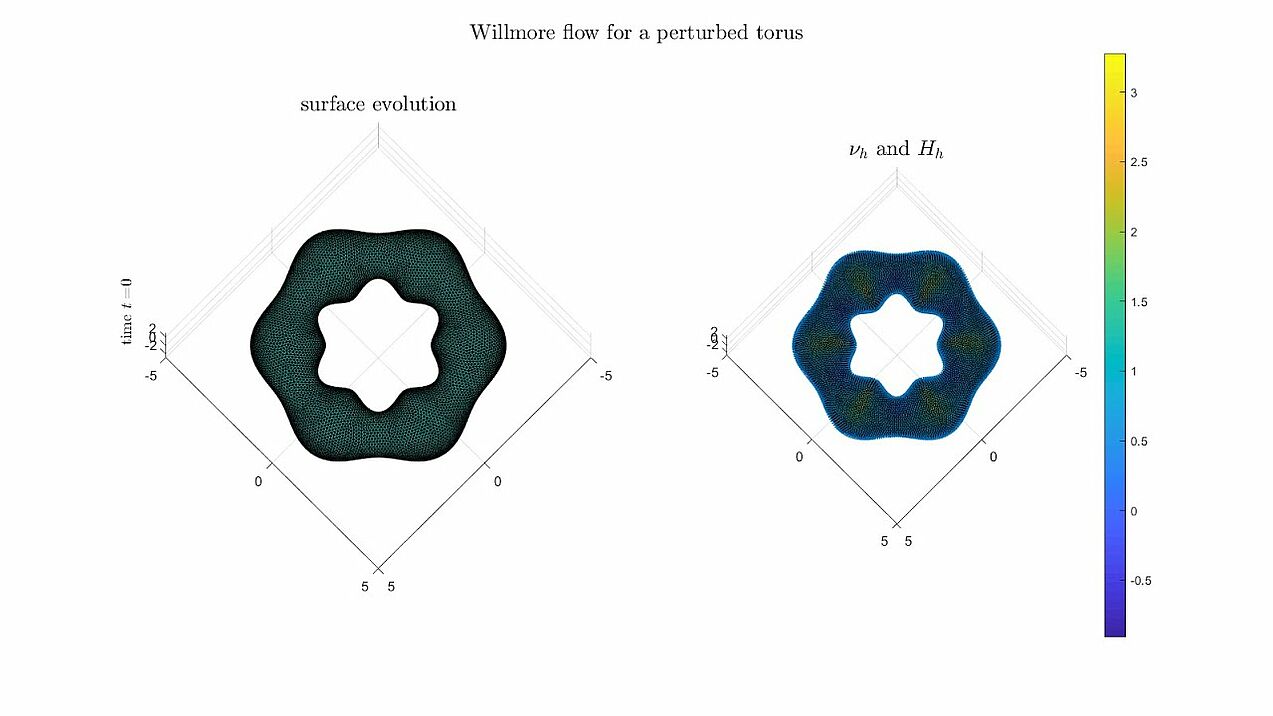
Willmore flow

Some numerical experiments for Willmore flow using the algorithm analysed in the paper.

Topologically spherical objects are known to converge to a sphere, while minimising the Willmore energy (W(\Gamma) \to 8\pi).
Surfaces of genus 1 are converging to a Clifford torus minimising the Willmore energy (W(\Gamma) \to 4\pi^2).

Willmore flow of a red blood cell

Willmore flow of a perturbed tours (top view)

Willmore flow of a perturbed torus towards a Clifford torus

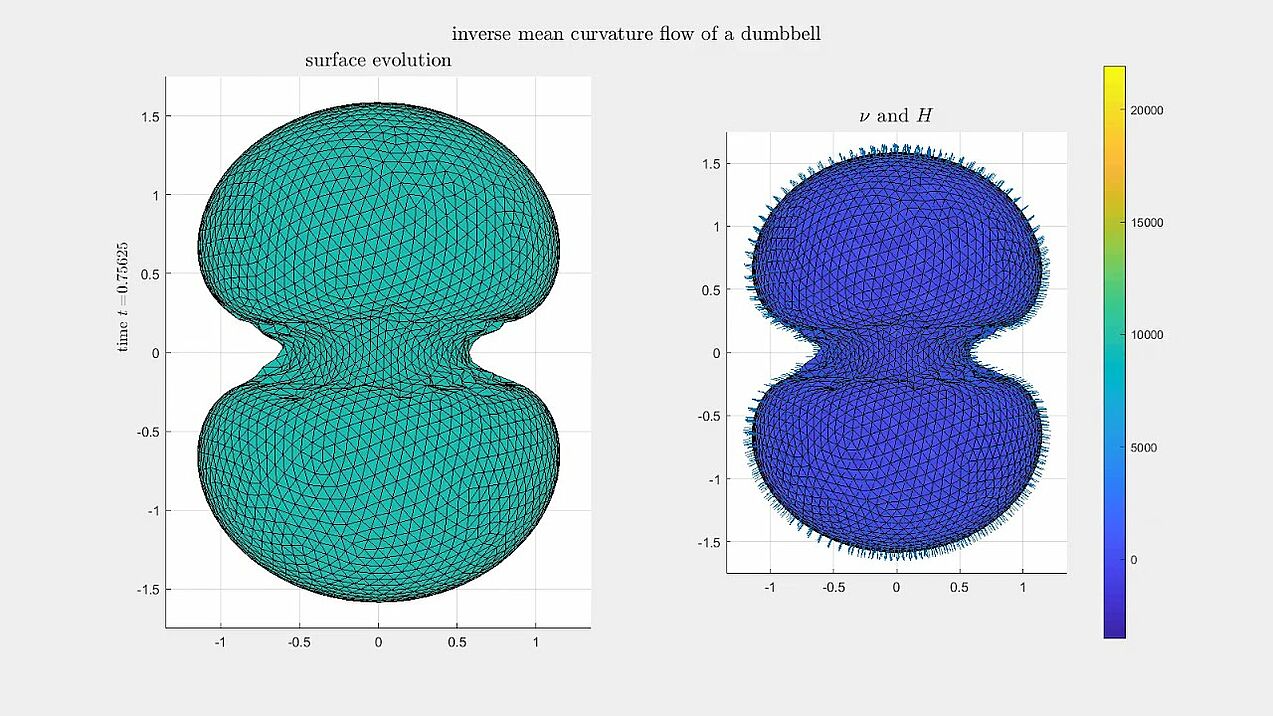
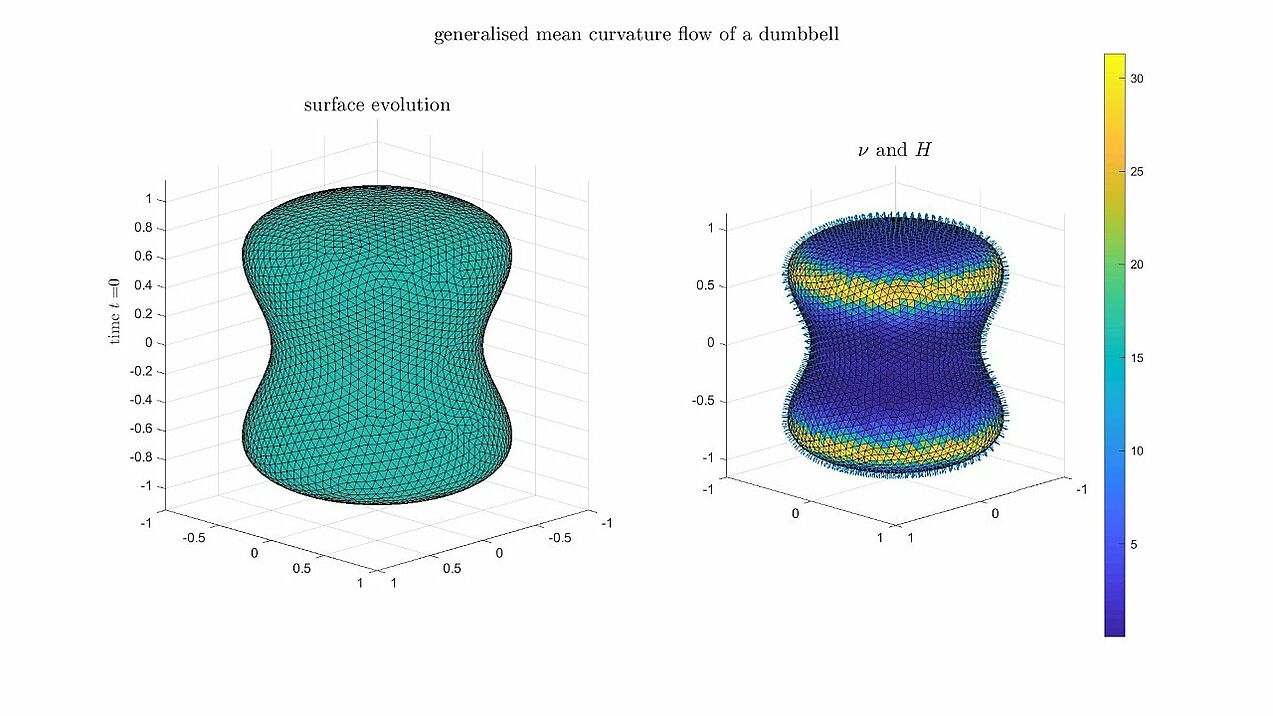
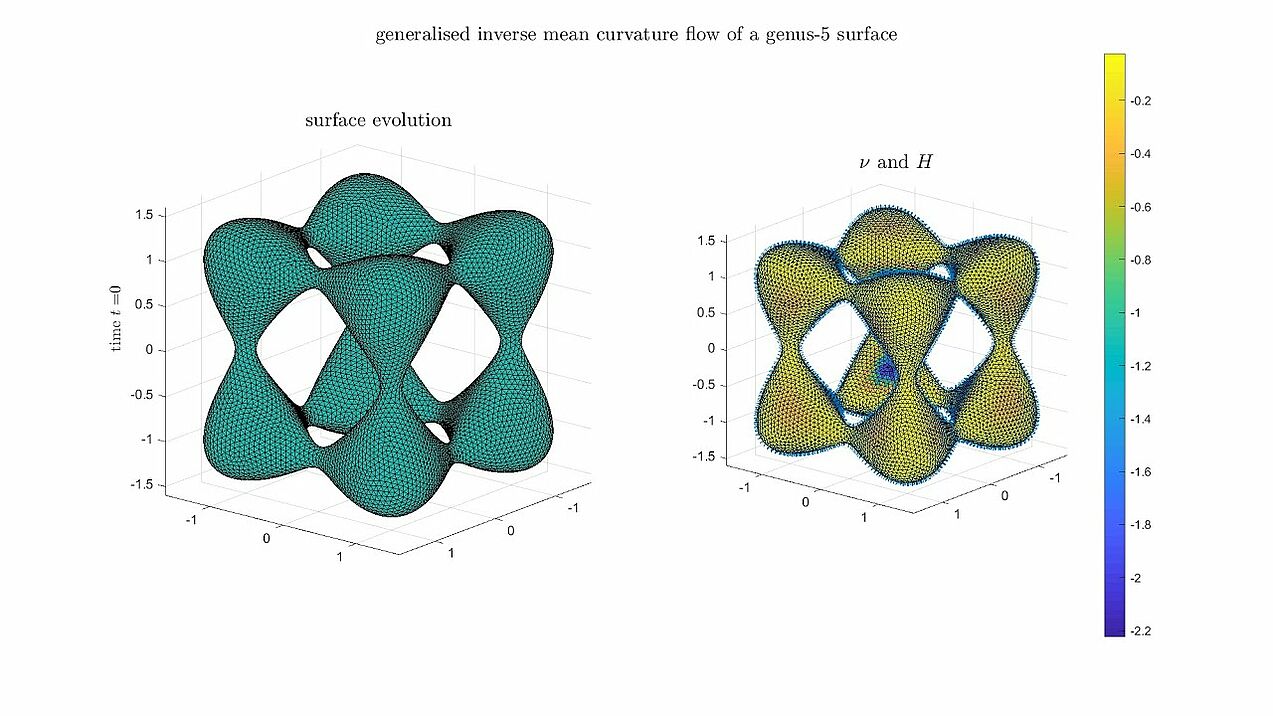
Generalised mean curvature flow

Numerical experiments for an algorithm for generalised mean curvature flows, i.e. the surface velocity is given by v = - V(H) \nu_\Gamma.

A non-convex dumbbell-shaped surface evolving towards a singularity along inverse mean curvature flow (V(H) = - 1 / H).

Inverse mean curvature flow of a dumbbell

A non-convex dumbbell-shaped surface evolving towards a pinch singularity along powers of mean curvature flow (V(H) = H^2)

Generalised mean curvature flow of a dumbbell

A genus-5 surface evolving under powers of inverse mean curvature flow (V(H) = - 1/H^2)

Generalised inverse mean curvature flow of a genus-5 surface

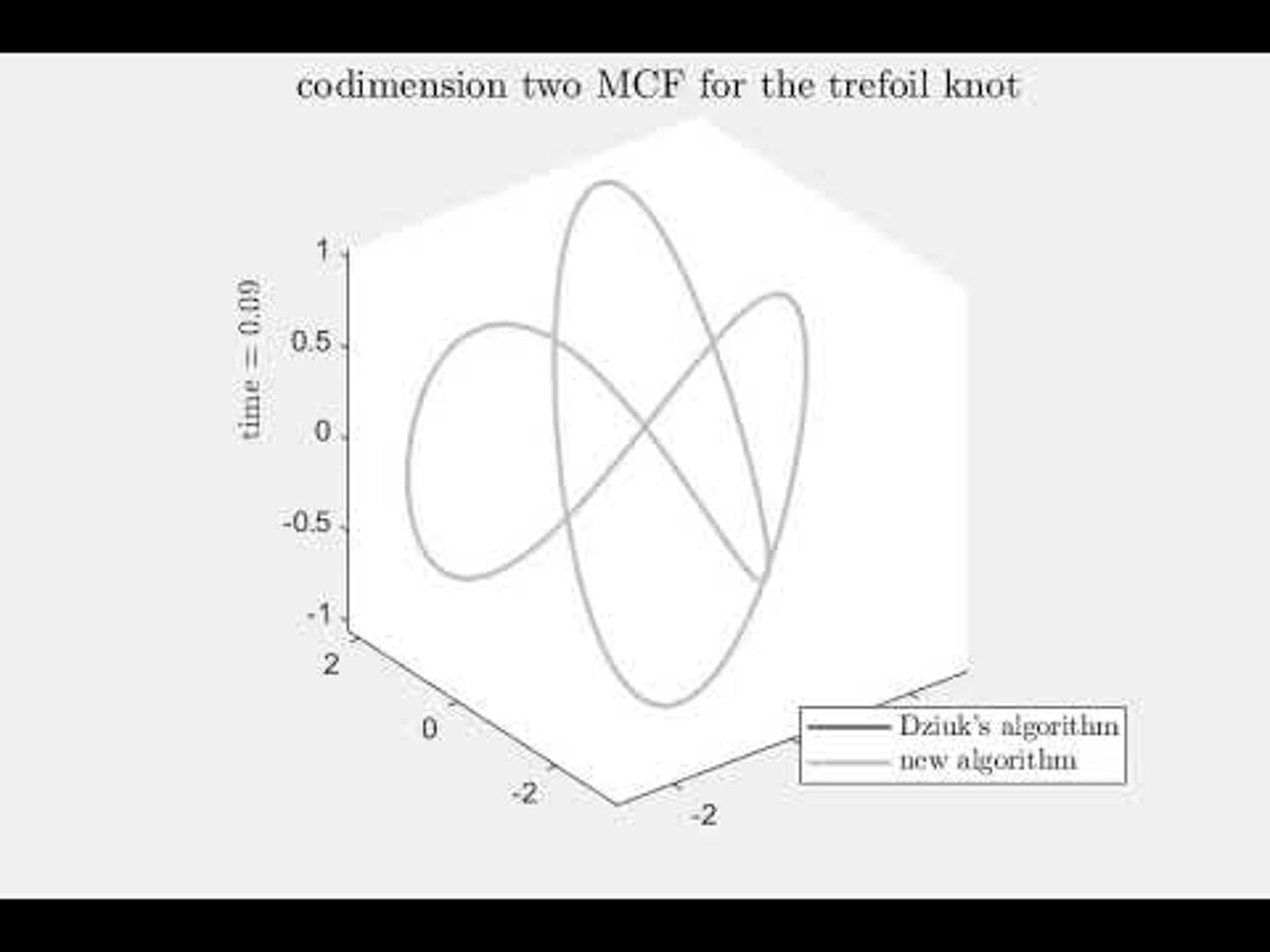
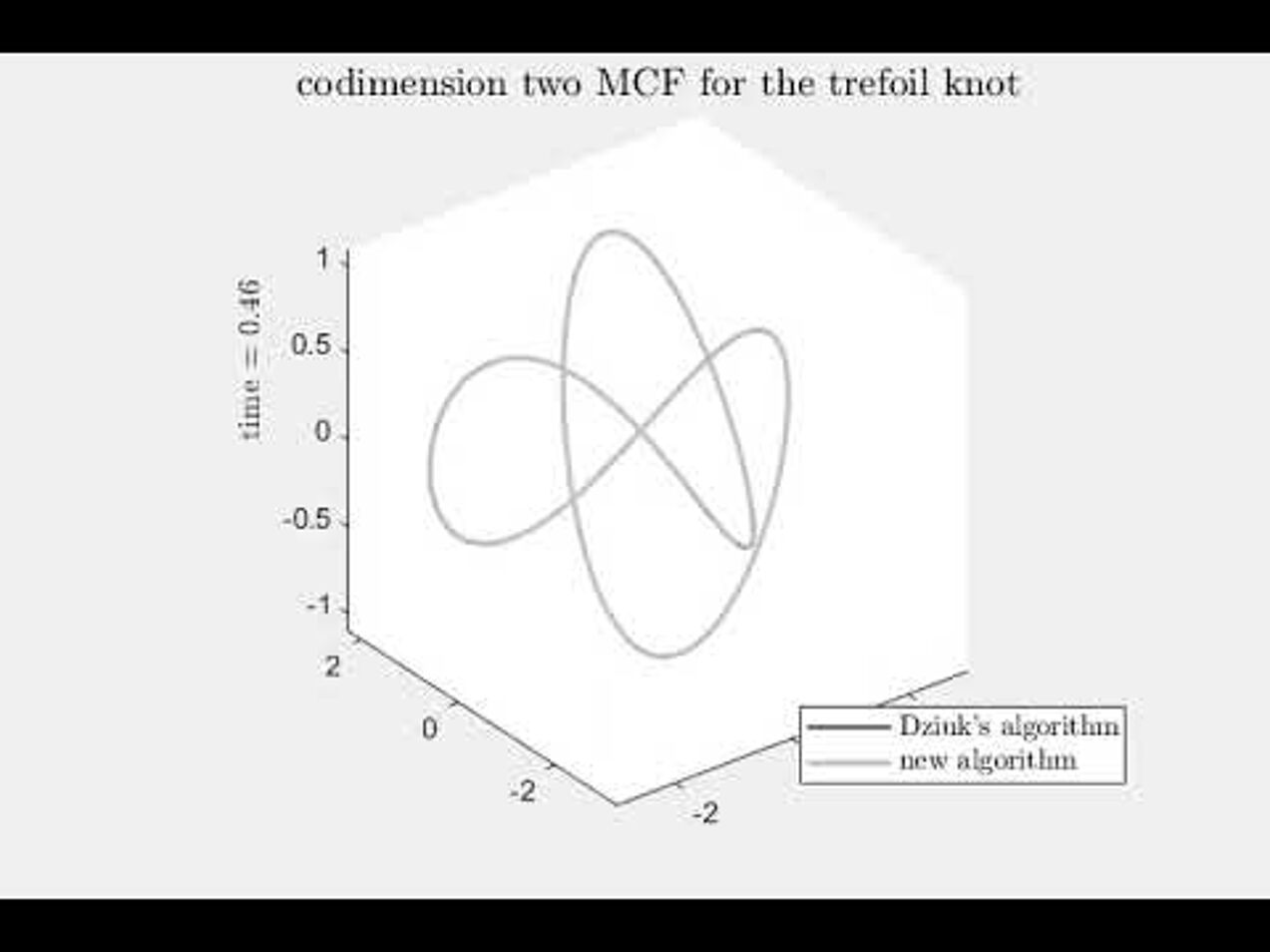
Mean curvature flow in higher codimension

Numerical experiments for an algorithm for mean curvature flow in codimension two.

A trefoil knot evolving under mean curvature flow in codimension 2.

Codimension 2 mean curvature flow of a trefoil knot (rescaled)

A trefoil knot evolving under mean curvature flow in codimension 2 (without rescaling)

Codimension 2 mean curvature flow of a trefoil knot

Mean curvature flow interacting with diffusion

Numerical experiments for an algorithm for the interaction of mean curvature flow and diffusion on closed surfaces. This model was first developed and studied by Bürger (University of Regensburg).

Mean curvature flow interacting with diffusion on an elongated ellipsoid.

Mean curvature flow interacting with diffusion - a singular flow

Mean curvature flow interacting with diffusion compared to pure mean curvature flow

Comparing mean curvature flow with diffusion-forced mean curvature flow

Numerical solutions for the mean curvature flow interacting with diffusion illustrating slow diffusion through a thin neck

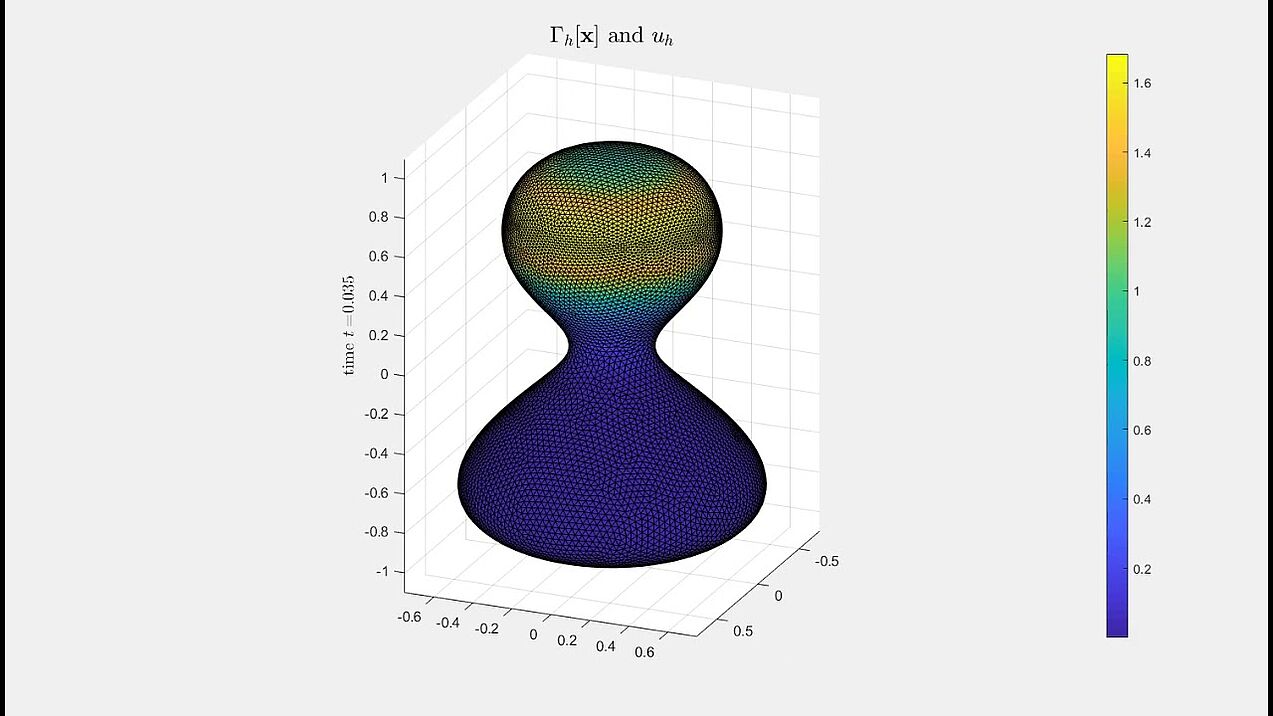
Mean curvature flow interacting with diffusion - Ecker's example

Numerical solutions for the mean curvature flow interacting with diffusion illustrating the possibility for self-intersecting solutions

Mean curvature flow interacting with diffusion - a self intersecting flow

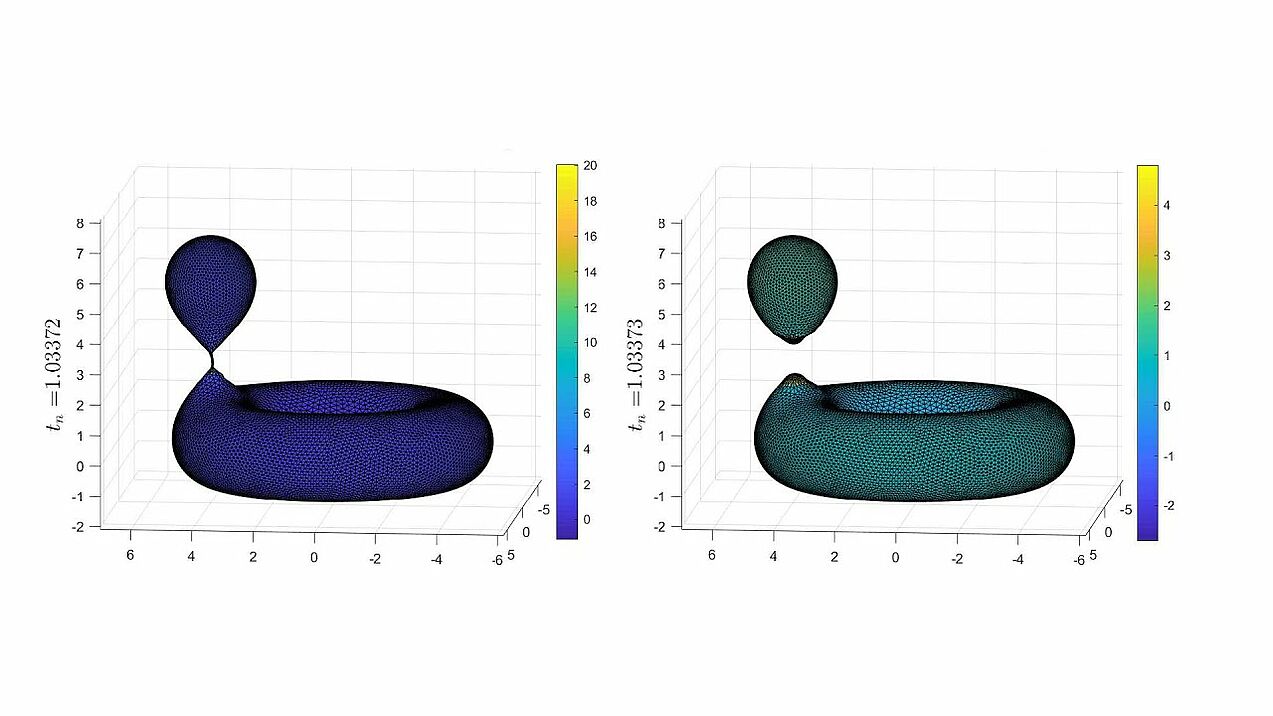
Numerical surgery for mean curvature flow

Inspired by surgery process of Huisken & Sinestrari and Brendle & Huisken, this paper proposes a numerical mean curvature flow algorithm with surgery for surfaces.

Resolving a pinch singularity of a dumbbell-shaped surface.

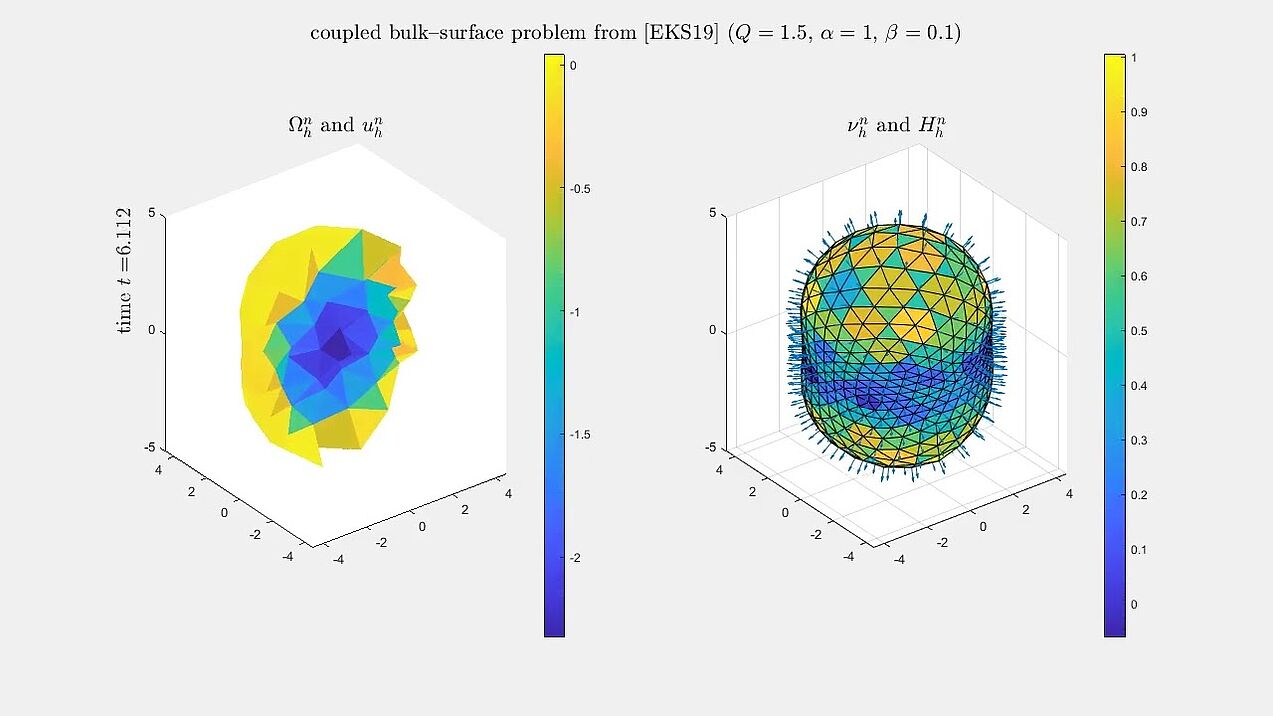
Numerical simulation of a tractable tumour growth model (alpha=1 beta=0.1)

Numerical surgery for a more complicated example of a torus and a sphere joined by a thin neck

Numerical surgery for mean curvature flow of a torus and a sphere joined by a thin neck

Numerical surgery for an inward collapsing fat torus (top view)

Numerical surgery for mean curvature flow for a torus merging into a sphere (top view)

Numerical surgery for an inward collapsing fat torus (intersection)

Numerical surgery for mean curvature flow for a torus merging into a sphere

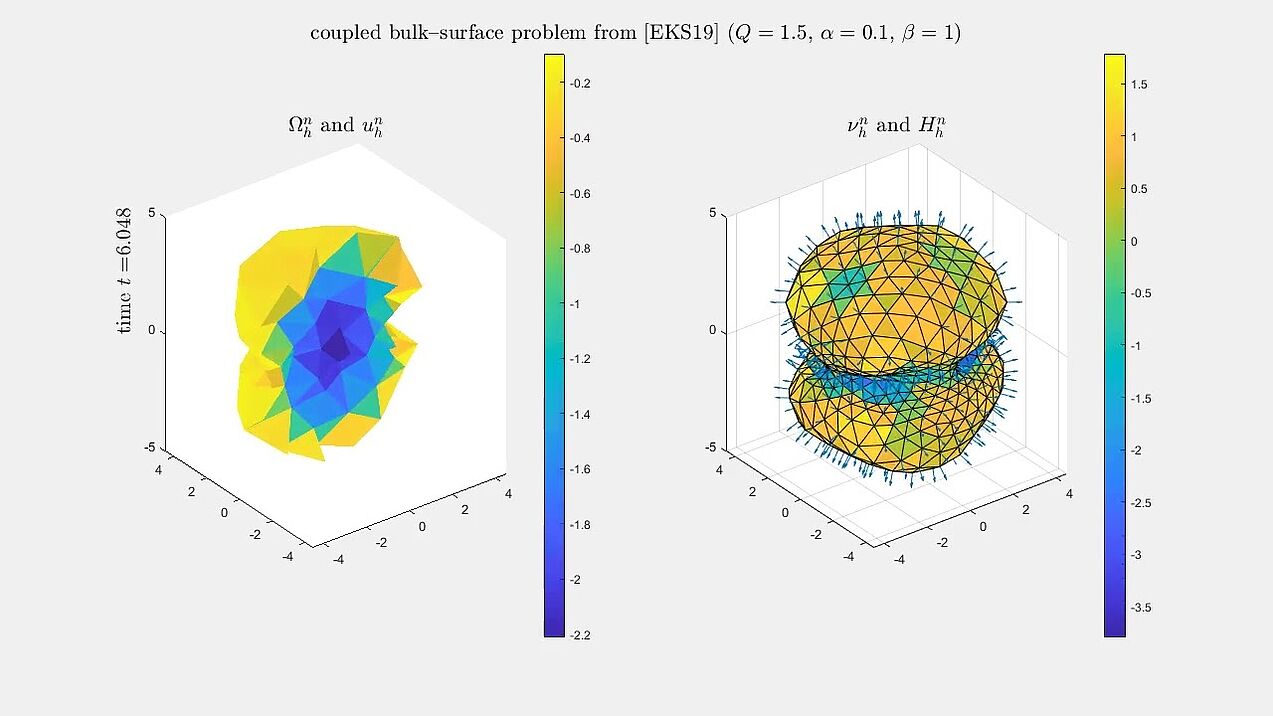
Bulk–surface model of tumour growth

Numerical simulations for an evolving bulk--surface finite element method for a model of tissue growth, which is a modification of the model of Eyles, King and Styles (2019).

Numerical simulation of a tractable tumour growth model (alpha=0.1 beta=1)

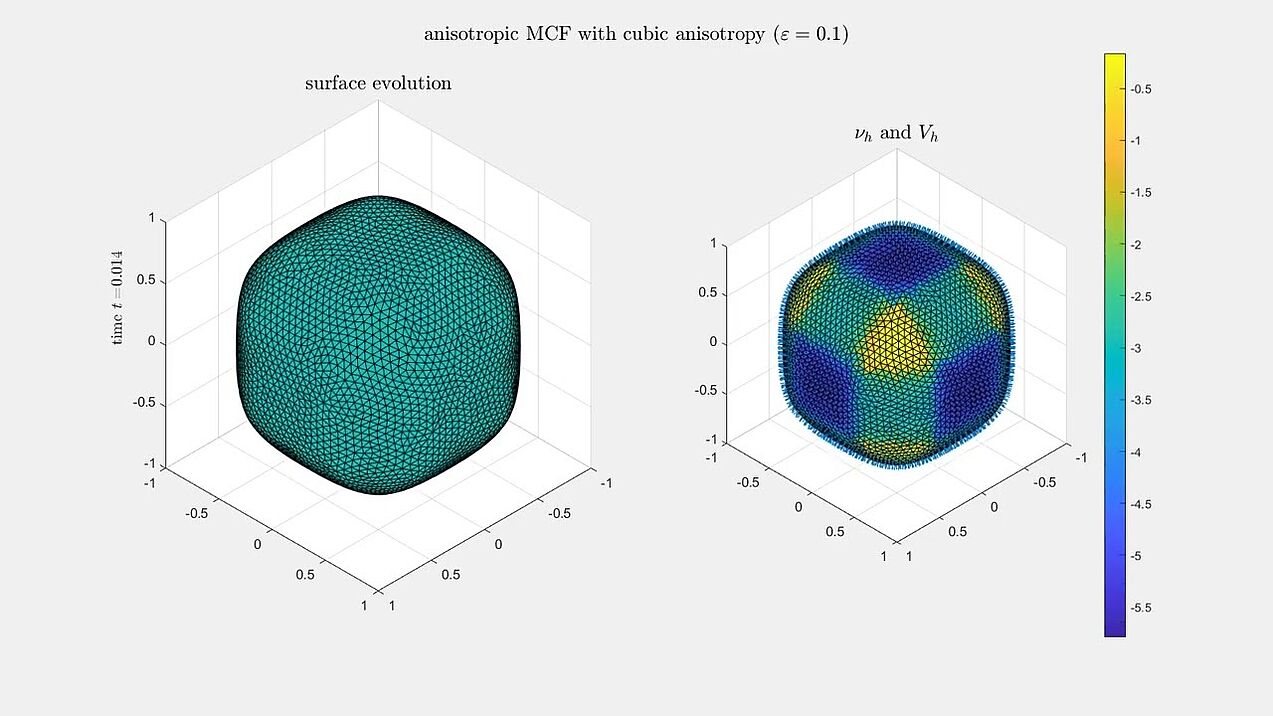
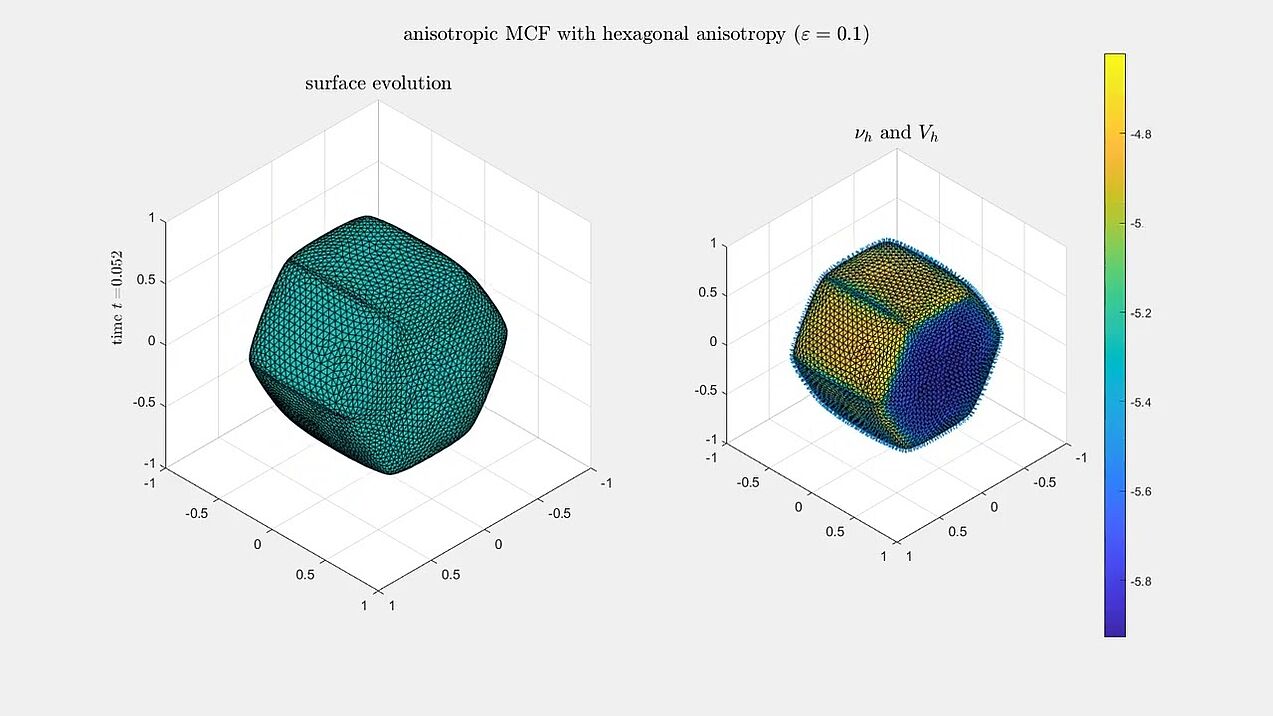
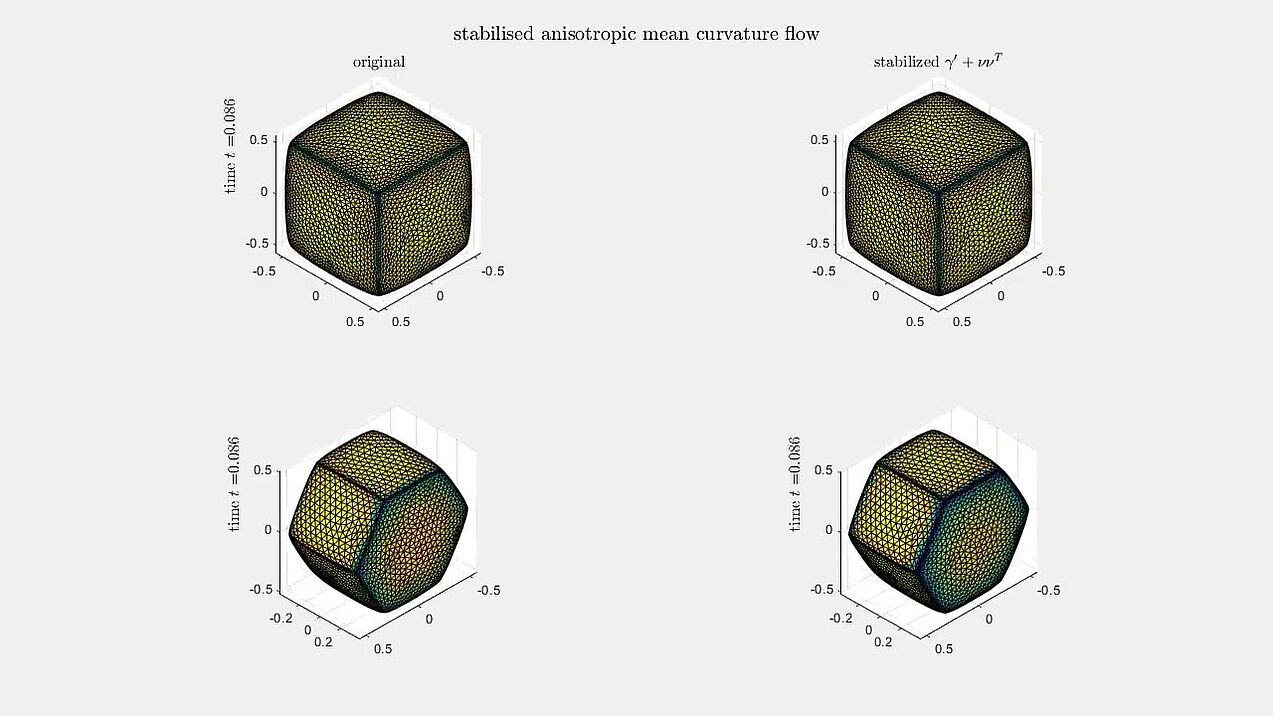
Anisotropic mean curvature flow

Numerical experiments for anisotropic mean curvature flow algorithm from our paper.

A sphere evolving under anisotropic mean curvature flow with a cubic and a hexagonal anisotropy.

Anisotropic mean curvature flow of a sphere with different anisotropies

Anisotropic mean curvature flow with a cubic anisotropy function

Anisotropic mean curvature flow with a hexagonal anisotropy function

Anisotropic mean curvature flow with stabilisation

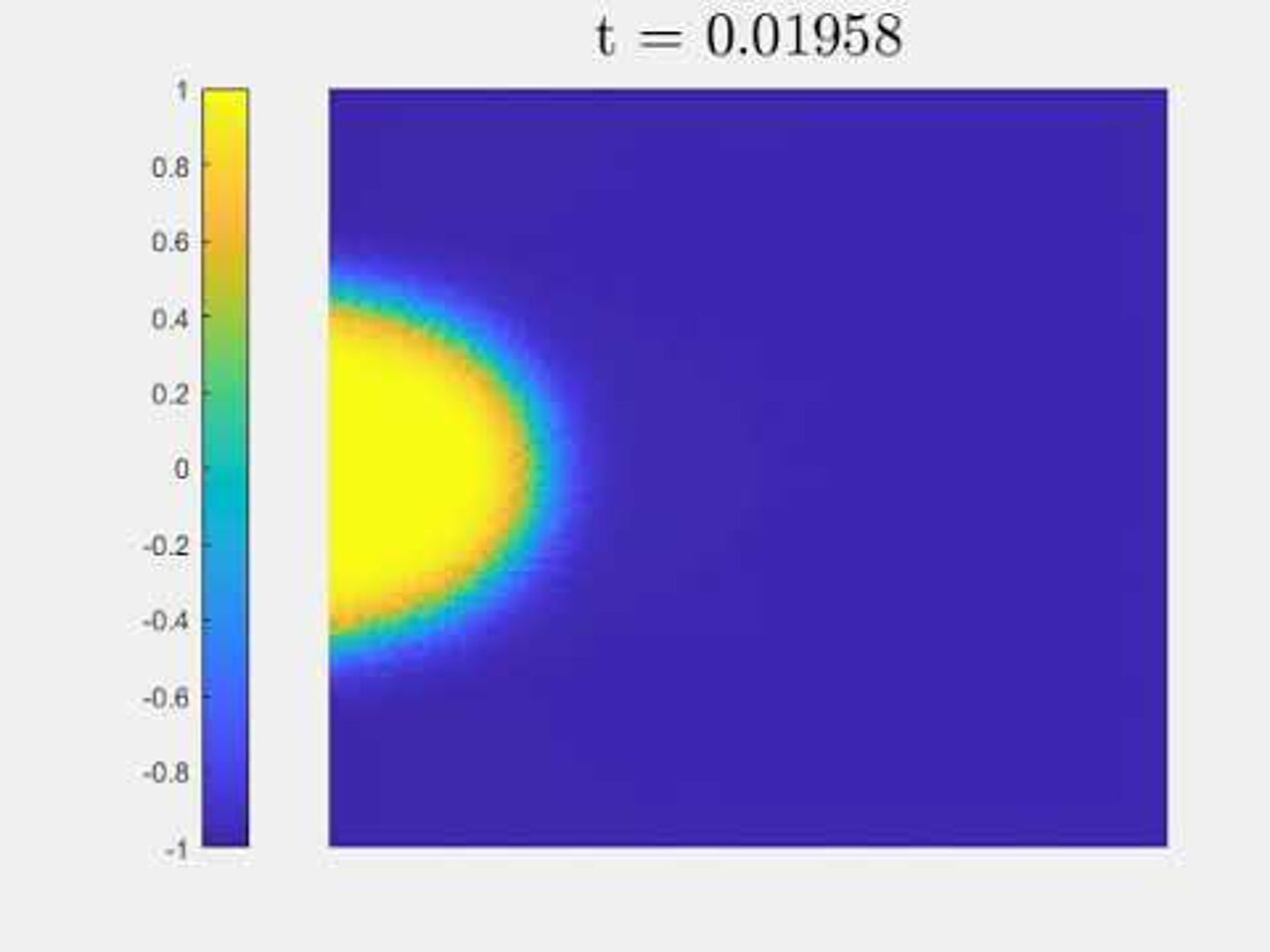
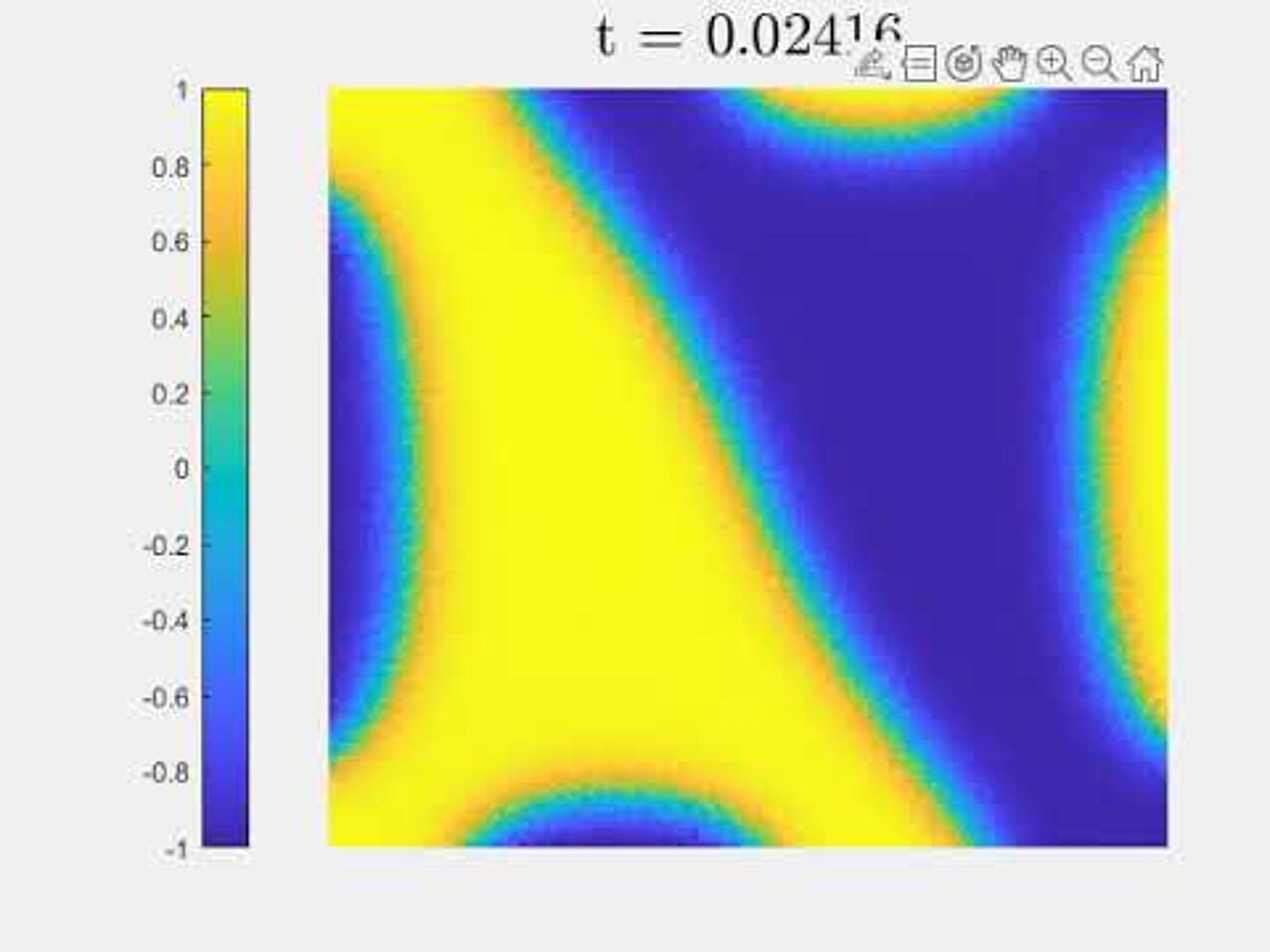
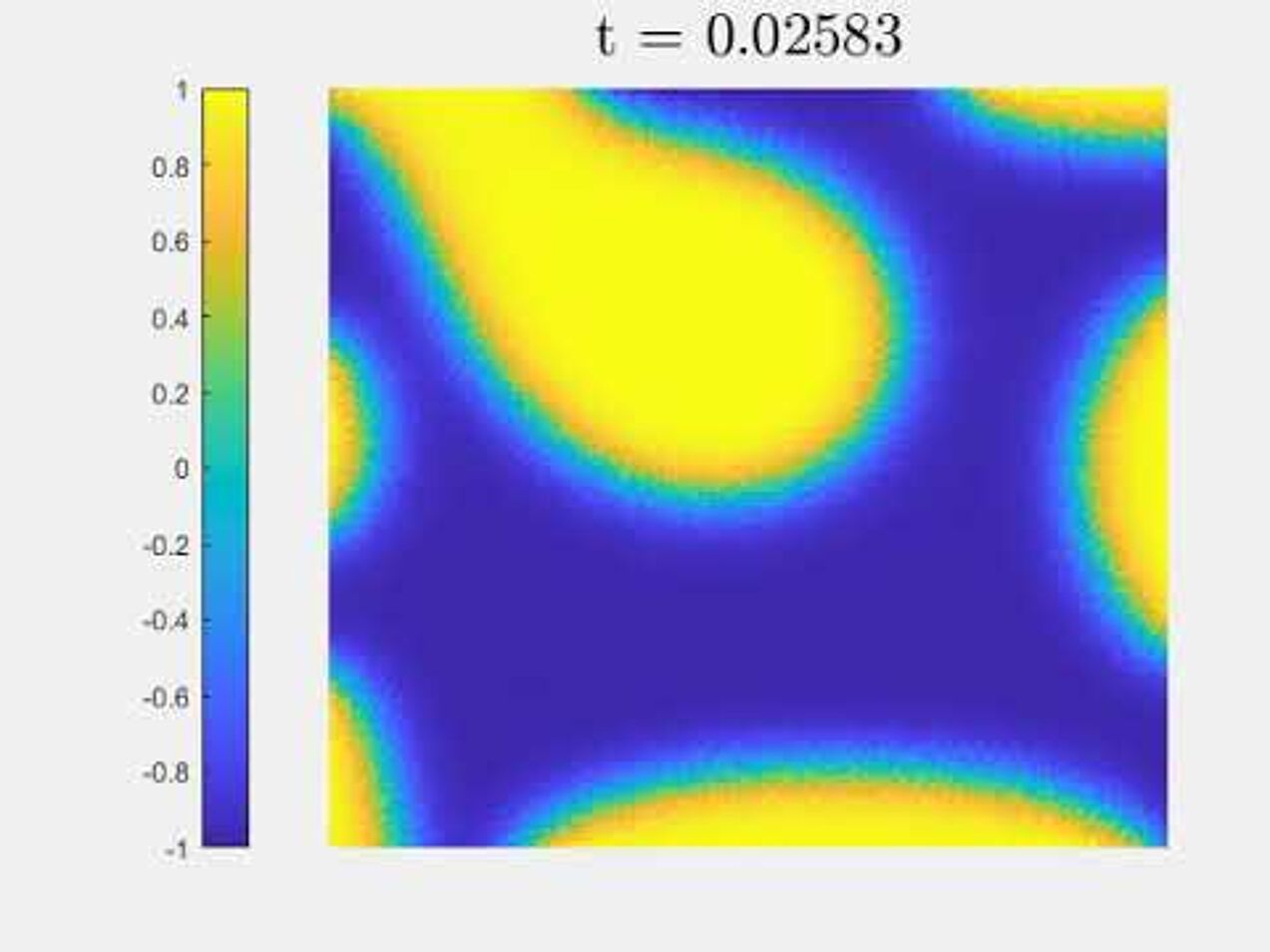
Cahn-Hilliard equation with dynamic boundary conditions

Numerical experiments for Cahn-Hilliard equation with dynmaic boundary conditions, with the algorithm from our paper.

An elliptically-shaped droplet evolving according to the GMS-model.

Evolution of a droplet according to the Cahn-Hilliard equation with dynamic boundary conditions

Evolution of a regular initial data

Evolution of a random initial data

Bulk-surface Cahn-Hilliard system with dynamic boundary conditions

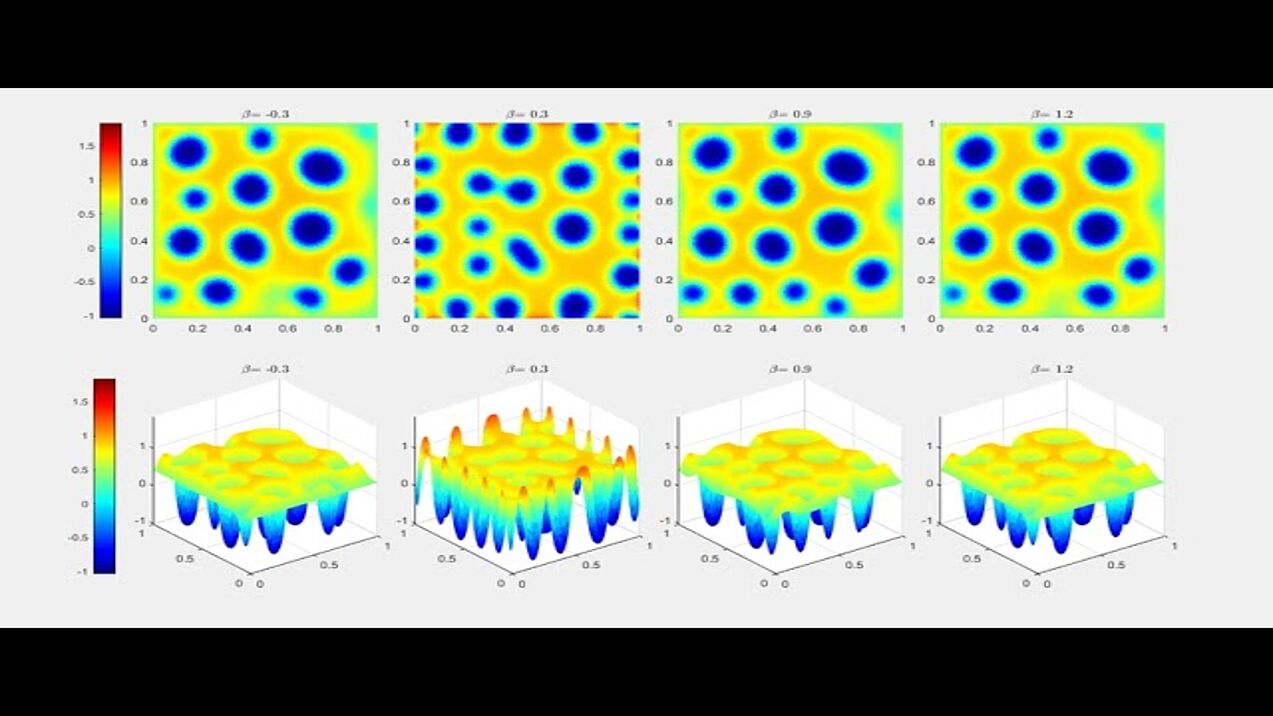
Numerical experiments for the bulk-surface Cahn-Hilliard system with general dynamic boundary conditions.

Evolution of a random initial data by the Cahn-Hilliard equation with transmission rate dependent dynamic boundary conditions with an affine linear transmission condition with constant parameter beta. Depending on the parameter beta we observe either Cahn-Hilliard phase-separation dynamics or near constant trace values.

Evolution of the Cahn-Hilliard equation with transmission rate dependent dynamic boundary conditions

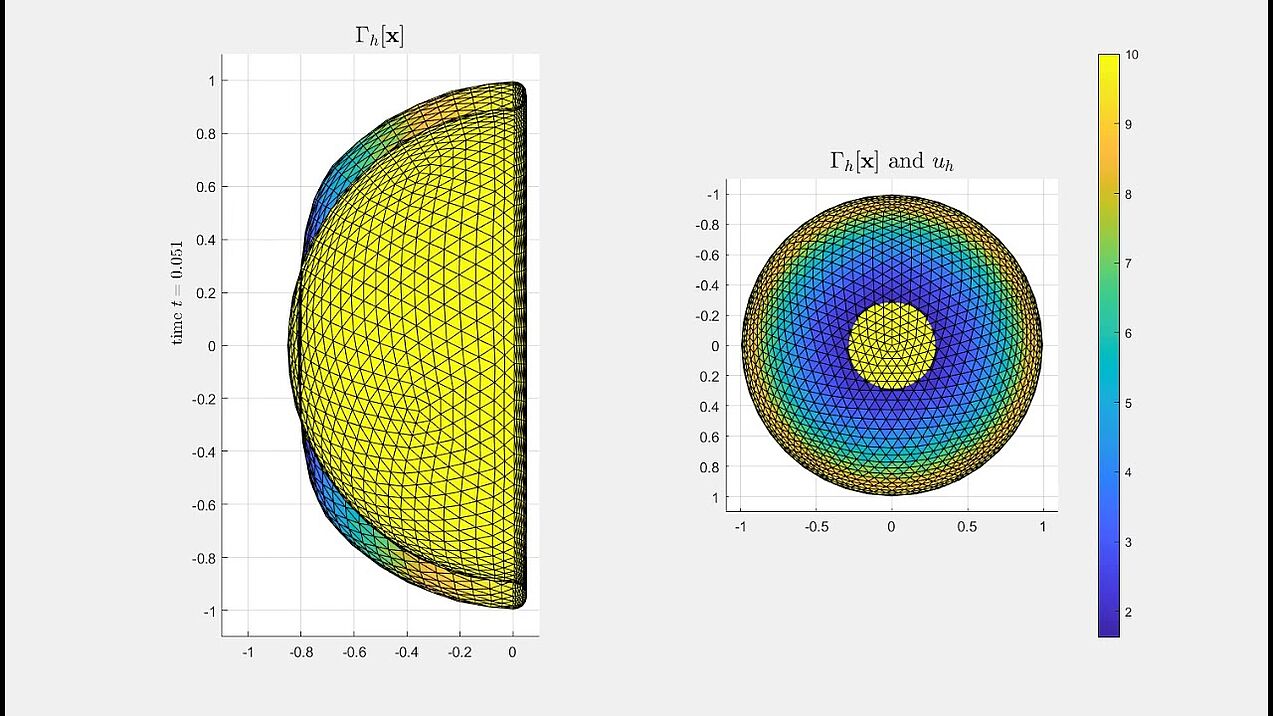
Adaptivity for parabolic PDEs on stationary surfaces

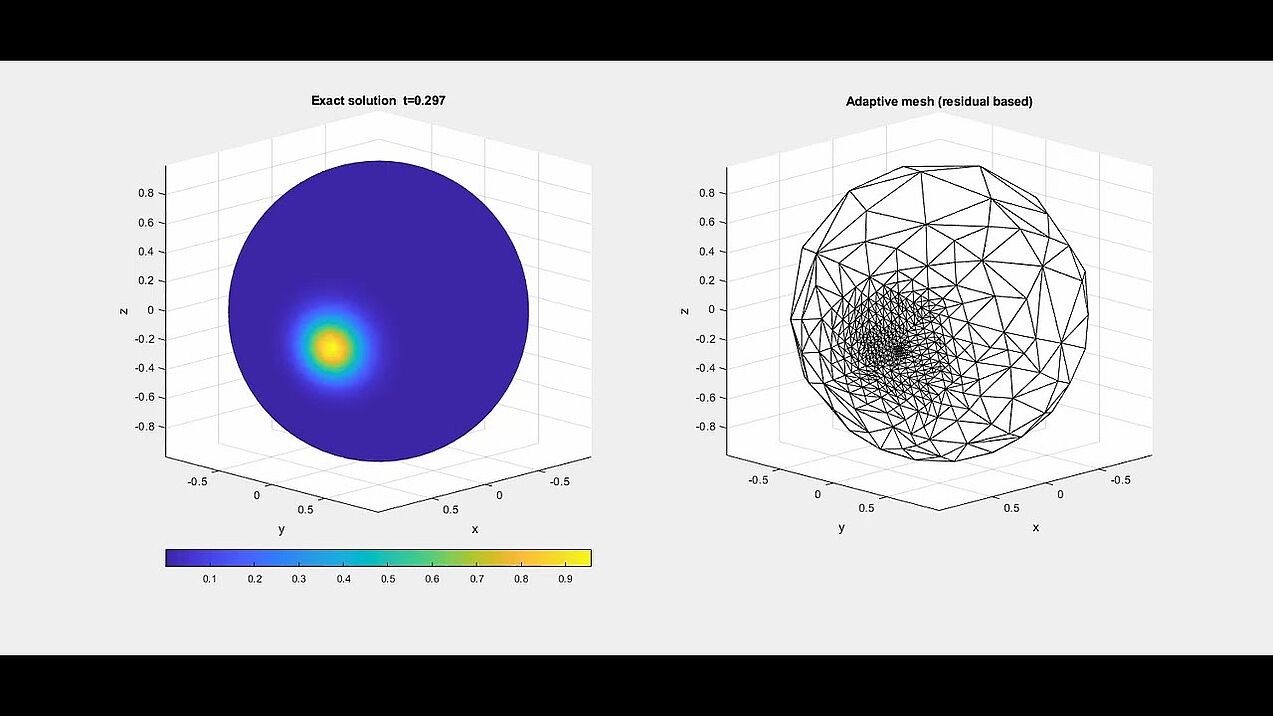
Numerical experiment of a residual based adaptive algorithm for parabolic PDEs on stationary surfaces.

We constructed an exact solution based on solving the parabolic heat equation on surfaces. This exact solution, a moving heat peak travelling along the equator while briefly vanishing for t=0.5, is presented on the left. The adaptive mesh for solving for the numerical solution, based on the residual based a posteriori error analysis, is given on the right.