Schritt 5: Op­ti­mie­rungs­pro­blem lö­sen

Nach der Auswahl geeigneter Algorithmen wird das Optimierungsproblem gelöst. Nachdem man sich vergewissert hat, dass die berechnete Lösung zu einer Verbesserung der Zielfunktion führt (durch Validierung des Systemmodells), kann diese nachfolgend im Rahmen der Betriebsphase des mechatronischen Systems genutzt werden.

Im Falle der optimalen Auslegung eines Hybridspeichers in einem Inselnetz wurden zwei Zielfunktionen formuliert (k=2). Die maximalen Kapazitäten der zwei Energiespeicher sind dabei die kontinuierlichen Optimierungsparameter (n=2), wobei die Speicherleistung hinreichend groß sein muss, damit es zu keiner Systeminstabilität kommt. Damit erhalten wir eine Nebenbedingung. Externe Parameter, sowie diskrete Optimierungsparameter sind jeweils nicht vorhanden (s=0, p=0). Bevor wir uns für die Auswahl eines Optimierungsverfahrens entscheiden können, müssen wir noch angeben, ob Ableitungen der Zielfunktionen sowie Nebenbedingung gegeben sind. In unserem Fall basieren sowohl die Zielfunktionen, als auch die Nebenbedingung auf der Auswertung eines MATLAB/Simulink Modells, für welches keine Ableitungen vorliegen. 
Damit erhalten wir folgendes Verfahren: das Unterteilungsverfahren basierend auf dem nicht-Dominanz-Test (Quelle: GAIO).

Damit das Unterteilungsverfahren eingesetzt werden kann benötigen wir des Weiteren:

• eine Berechnungsvorschrift für die Zielfunktionsauswertungen
• eine Berechnungsvorschrift für die Auswertung der Nebenbedingung(en)
• obere und untere Grenzen für die Optimierungsparameter
• Anzahl der Unterteilungsschritte sowie Anzahl der Testpunkte pro Box.

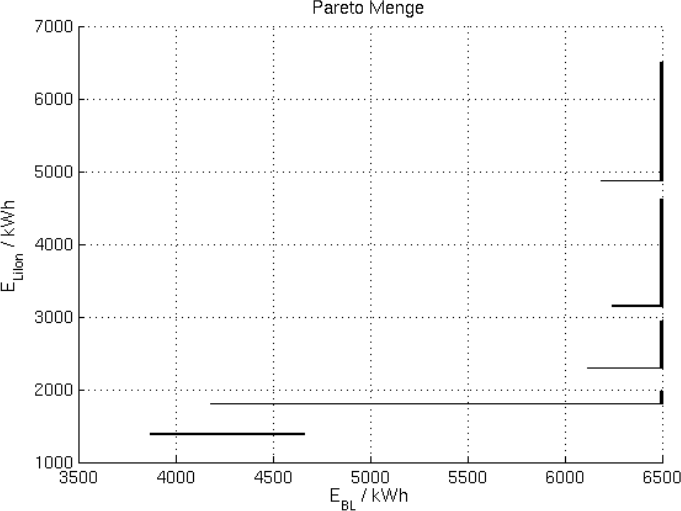
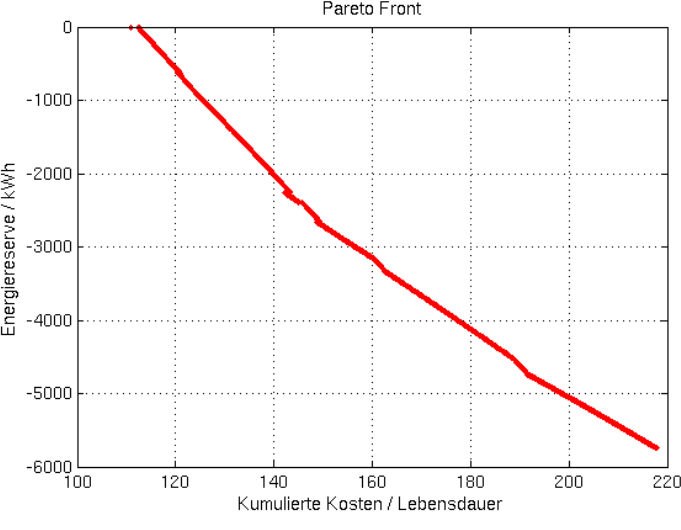
Als Resultat erhalten wir die folgende Pareto-Menge und Pareto-Front: 

Sie sollten am Ende folgendes haben: Gelöstes Optimierungsproblem

Wenn Sie dies haben, dann klicken Sie auf den nachfolgenden Link für den nächsten Schritt.

weiter zu Schritt 6