Sup­ple­ment­ary Ma­ter­i­al for "Mero­morph­ic Con­tinu­ation of Weighted Zeta Func­tions on Open Hy­per­bol­ic Sys­tems"

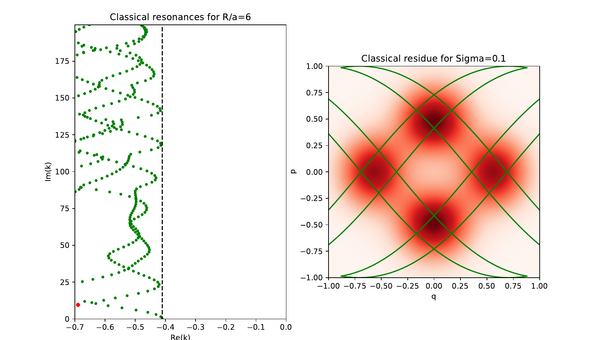
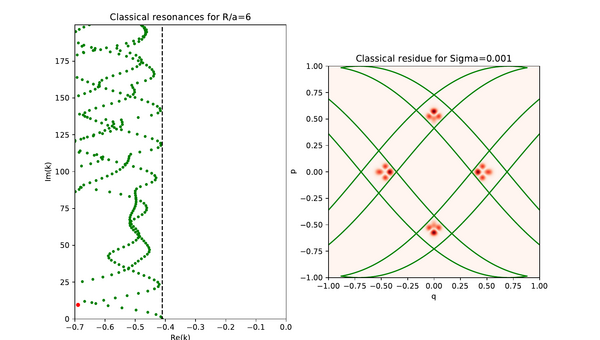
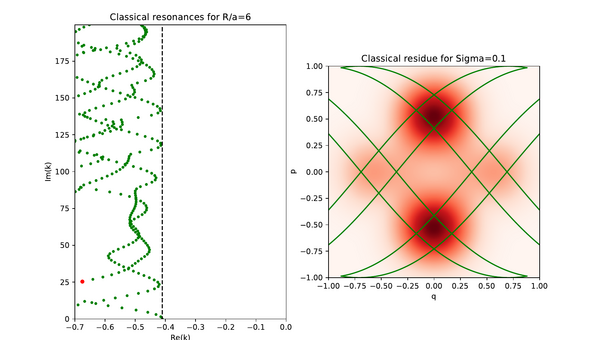
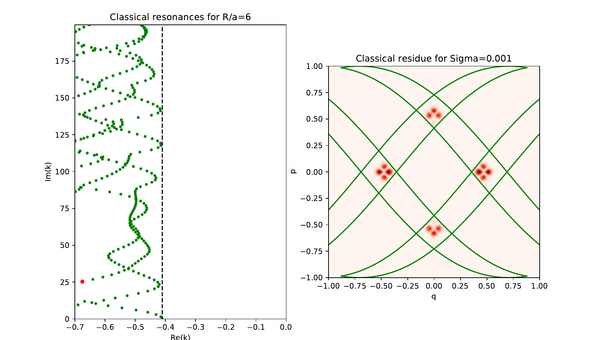
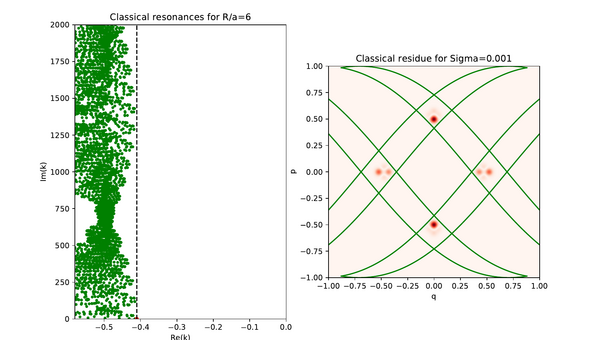
This page contains supplementary material regarding invariant Ruelle distributions for the paper "Meromorphic Continuation of Weighted Zeta Functions on Open Hyperbolic Systems" by Schütte/Weich. We present three different categories of plots of invariant Ruelle distributions for the case of a 3-disc system with R/a = 6 below (the geometric setting is shown on the left). Instead of plotting on the full phase space of dimension three we restricted the distributions to a 2-dimensional Poincarè section with coordinates (q, p) for computational reasons as well as for ease of graphical presentation. Every plot has an additional parameter, namely the width of the Gaussians used to approximate the distributions, and the spectral parameter is denoted as k.

For more information please refer to the description of a specific video.

This video illustrates plots of invariant Ruelle distributions along a resonance chain. The distribution is shown on the right, while the associated resonance is highlighted in red on the left. In this as well as in all following videos we marked the intersection of the second-order trapped set with the Poincarè section in green. Notice how the invariant Ruelle distributions seem to exhibit oscillatory dynamics along the chain.

The width parameter was chosen to be 0.1 for this video.

This video illustrates the same resonance chain as the first one, but this time with much small width equal to 0.001. One clearly sees the concentration of the invariant Ruelle distributions on a smaller scale of the fractal trapped set.

This video illustrates the dynamical behavior of invariant Ruelle distributions along a second resonance chain. The width in this video is 0.1.

Here we plotted the dynamics along the same resonance chain as in the third video, but with a smaller Gaussian width of 0.001.

Here we compare the invariant Ruelle distributions at resonances near the spectral gap (marked with the dashed vertical line). The closer a resonance comes to the spectral gap the more similar its phase space distribution appears to the distribution associated with the first resonance on the real line.

This plot again uses a Gaussian width of 0.001.