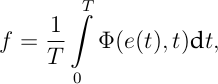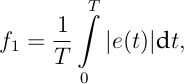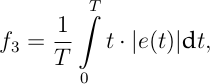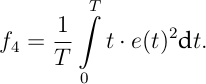Fehlerintegrale und zeitgewichtete Fehlerintegrale
Möchte man eine optimale Regelung erzielen, so ist der klassische Ansatz für eine Bewertungsfunktion die Regelabweichung, also die Bewertung der Dynamik des Systems über der Abweichung zwischen des Systemausgangs y(t) und einer gegebenen Referenzgröße w(t):
Für einen vorgegebenen Zeithorizont [0,T] wird diese Abweichung e in Form eines integralen Gütekriteriums zusammengefasst. Dementsprechend können wir unsere Zielfunktion f:Rn → R definieren als:
wobei über die Abbildung Φ:R → R Kompromisslösungen zwischen einem überdämpften und einem ungedämpften System definiert werden können, in dem quadratische Fehlerintegrale oder Betragsfehlerintegrale als Zielfunktion minimiert werden. Dabei werden Dauerschwingungen in beiden Fällen ebenso bestraft, wie ein langsames überdämpftes Annähern der Referenzlösung w(t). Im Folgenden betrachten wir die am häufigsten benutzten Betragsfehlerintegrale [2] für unterschiedliche Abbildungen Φ.
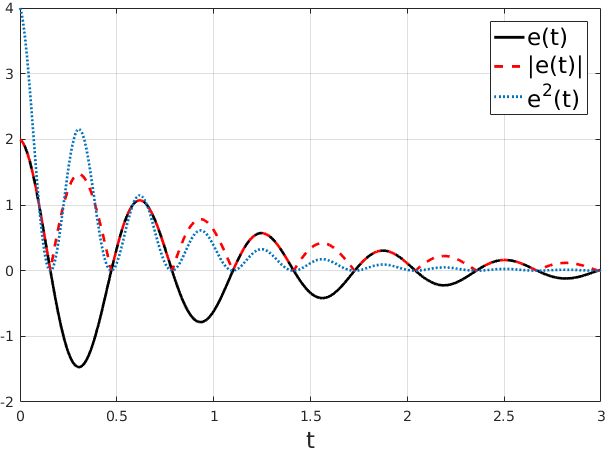
Bei den zeitgewichteten Betragsfehlerintegralen, d.h. Φ(e(t), t) = |e(t)|,
wird das Integral sowohl für positive als auch negative Abweichungen erhöht. Große Anfangsabweichungen, wie sie z.B. bei Sprungantworten auftreten, fallen dabei relativ stark ins Gewicht. Insgesamt erhalten wir ein gering gedämpftes System.
Bei den quadratischen Fehlerintegralen, d.h. Φ(e(t), t) = e(t)2,
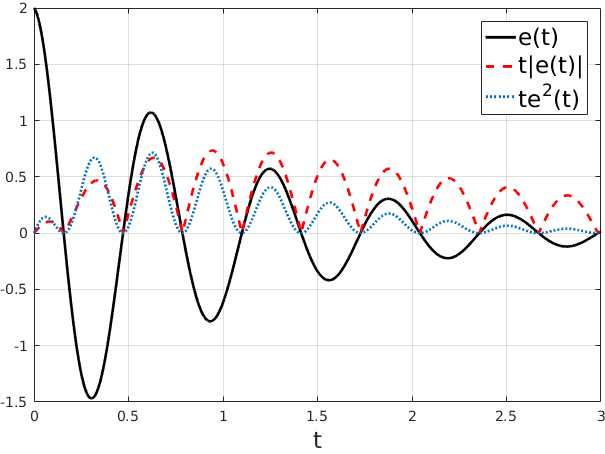
werden hohe Regelabweichungen stärker bestraft was daher tendenziell zu einem schnelleren, aber weniger stark gedämpften System führt. Vor allem die großen Anfangsabweichungen fallen hier sehr stark ins Gewicht. Um den großen Einfluss dieser anfänglichen Fehler zu reduzieren und im Weiteren Abweichungen nach langer Zeit stärker zu bestrafen bietet sich eine zeitliche Gewichtung der Fehlerintegrale an. Die am häufigsten verwendeten zeitlich gewichteten Fehlerintegrale sind dabei
In der unteren Abbildung werden die jeweiligen Unterschiede veranschaulicht. Als Beispiel wurde e(t) = 2 exp(−t) · cos(10t) gewählt um den Effekt der Zeitgewichtung besser hervorzuheben. Für mechatronische bzw. selbstoptimierende Systeme besitzen Betragsfehlerintegrale und quadratische Fehlerintegrale höchste praktische Bedeutung [4]. Für die Bewertung eines Einschwingvorgangs liefern erfahrungsgemäß die zeitgewichteten Fehlerintegrale sehr gute Ergebnisse. Diese sind jedoch nur dann sinnvoll einsetzbar, wenn die Anregungs- bzw. Referenzsignale ein eindeutiges Startereignis und einen stationären Verlauf gegen Ende des Bewertungszeitraums besitzen. Ist das Ergebnis bekannt, so lässt sich der Start der zeitlichen Gewichtung festlegen. Hierfür werden Sprungfunktionen, seltener auch Rampenfunktionen verwendet. Liegt keine Zeitgewichtung vor, können beliebige Anregungsfunktionen verwendet werden, wie z. B. Rauschsignale oder periodische Signale wie Sinusschwingungen oder Rechtecksignale.
Hier geht es weiter mit typischen Zielfunktionen die auf punkt- und abschnittsweise bewertenden Kriterien basieren.
| Einleitung |
| Fehlerintegrale und zeitgewichtete Fehlerintegrale |
| Punkt- und abschnittsweise bewertende Kriterien |
| Optimale Regelung |
| Modellprädiktive Regelung |
| Referenzen |