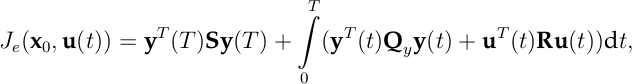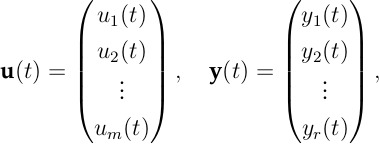Op­ti­male Steuer­ung

Bezieht sich die Güteforderung auf den gesamten Verlauf der Stell- bzw. Regelgrößen wird die optimale Steuerung in Betracht gezogen, bei der ein Gütefunktional J als Maß für die Güte des Regelkreises herangezogen wird. Im Folgenden wird Kapitel 7.1 aus [3] zusammengefasst.

Das Gütefunktional wird im Allgemeinen als quadratisches Funktional definiert

wobei im vorgegebenen Zeitintervall 0 ≤ t ≤ T der Verlauf der Stellgröße u(t) und der Regelgröße y(t) bewertet wird, sowie der zu der Endzeit T erreichte Wert y(T) der Regelgröße. Dabei sind die Matrizen S, Q_y und R symmetrisch und positiv (semi)definit, wodurch alle Summanden nichtnegativ sind. Des Weiteren wird hier angenommen, dass es sich um ein Mehrgrößensystem handelt, d.h.

und die optimale Steuerung zusätzlich vom Anfangszustand x₀ abhängt. Das Ziel der optimalen Regelung ist es eine Funktion u^*(t) zu finden, für die das Gütefunktional den kleinstmöglichen Wert annimmt:

Zusammenfassend erhält man eine optimale Steuerung u^*(t), welche das zugrunde liegende System aus dem Anfangszustand x₀ in bestmöglicher Weise im Zeitintervall 0 ≤ t ≤ T in einen Endzustand x(T) überführt. Je größer dabei die Werte von u(t) und y(t) sind, umso größer ist das Integral, wobei durch die quadratischen Terme große Werte stärker bestraft werden als kleine. Man interpretiert das obige Gütefunktional deshalb auch als verallgemeinertes quadratisches Regelintegral.

Hier geht es weiter mit typischen Zielfunktionen der modellprädiktiven Regelung.