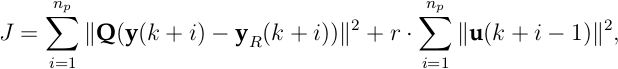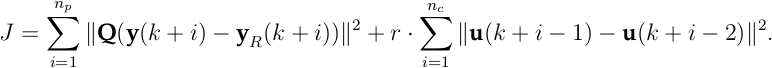Mod­ell­prädikt­ive Re­gel­ung

Die letzte Klasse von typischen Zielfunktionen im Bereich der mechatronischen bzw. selbstoptimierenden Systeme sind die Zielfunktionen, die bei modellprädiktiven Regelungen (MPC, [5]) zum Einsatz kommen. Liegen mathematisch formulierte Prozessmodelle vor, so erlauben diese unter Anderem die Prädiktion des zukünftigen Verhaltens. Im Folgenden wird ein oft verwendetes Gütefunktional vorgestellt, wobei die Notationen und Formulierungen aus [1] entnommen sind.

Die am häufigsten in der industriellen Praxis eingesetzten modellprädiktiven Regelungen basieren auf linearen Prozessmodellen, die auf das folgende quadratische Gütemaß angewendet einen linearen Regler ergeben:

oder

Dabei wird mit Q eine positiv definite Matrix bezeichnet, die oft eine Diagonalmatrix ist (Diagonalelemente d_ii > 0). Des Weiteren wird n_p der Prädiktionshorizont und n_c der Stellhorizont genannt. Mit y_R wird hier der Referenzverlauf bezeichnet. Wie schon in der optimalen Regelung liegt auch hier ein Mehrgrößensystem vor.
Nach geeigneter Transformation erhält man für lineare Prozessmodelle das konvexe Gütemaß

wobei mit ∆ū die Änderungsrate der Stellgrößen bezeichnet wird. In der industriellen Praxis findet die lineare modellprädiktive Regelung Verwendung, wenn die zu optimierenden Variablen zusätzlichen Beschränkungen unterliegen, z. B. im Stellgrößenvektor, d. h. u_min ≤ u(k) ≤ u_max. Von Bedeutung sind des Weiteren Beschränkungen der Änderungsrate der Stellgrößen, d.h. Beschränkungen der Art

oder aber Beschränkungen der Zustandsgrößen x_i oder der Ausgangsgrößen y_i .