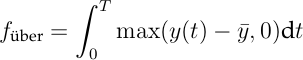Punkt- und abschnittsweise bewertende Kriterien
Die nächste häufig verwendete Klasse an Bewertungskriterien, welche wir betrachten, sind punkt- und abschnittsweise bewertende Kriterien. Im Unterschied zu den Fehlerintegralen wird hier das System nicht am gesamten Zeitverlauf [0,T] gemessen, sondern nur anhand einzelner Zeitpunkte bzw. Zeitabschnitte. Mit punktweise bewertenden Funktionen werden einzelne Ereignisse im Zeitverlauf der Simulation detektiert. Die Zielfunktionswerte ergeben sich in diesem Fall aus der Simulationsgröße zu einem bestimmten Zeitpunkt. Wichtige punktweise definierte Funktionen sind das Maximalwertkriterium, welches den größten Überschwinger der Sprungantwort beurteilt und damit ein mögliches Maß für Dämpfung darstellt, sowie verschiedene Triggerkriterien, die die Schnelligkeit des Systems angeben. Das Schwellwertkriterium ist ein abschnittsweise bewertendes Kriterium und wird eingesetzt, um das Überschreiten vorgegebener Grenzen graduell zu bestrafen.
Im Folgenden wird eine mathematische Formulierung aller Kriterien angegeben, sowie deren Bedeutung anhand einer Sprungantwort eines PT2-Gliedes illustriert (vgl. [4]). Die Sprungantwort y(t) des PT2-Glieds ist gegeben durch
wobei mit K = 2 der Verstärkungsfaktor, T̃ = 0.1 die Zeitkonstante und d = 0.1 die dimensionslose Dämpfung bezeichnet wird.
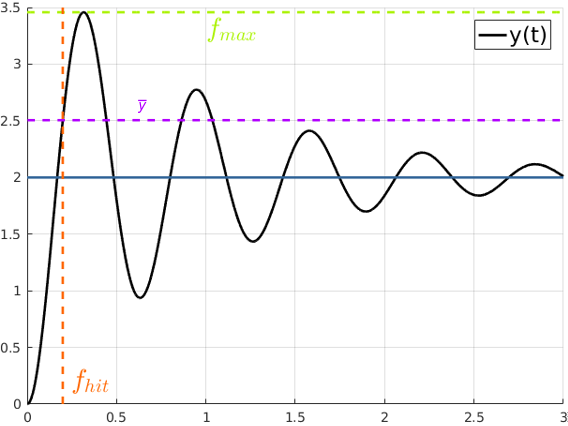
Das Maximalwertkriterium ermittelt den maximalen während der Simulation auftretenden Funktionswert im Zeitintervall [0,T]:
Im Unterschied dazu ermittelt die folgende Triggerfunktion den Zeitpunkt t̄, bei dem ein bestimmter Schwellwert ȳ zum ersten Mal erreicht wird:
Mit anderen Worten: fhit = t̄. Diese beiden Kriterien sind in Abbildung 2.1 veranschaulicht.
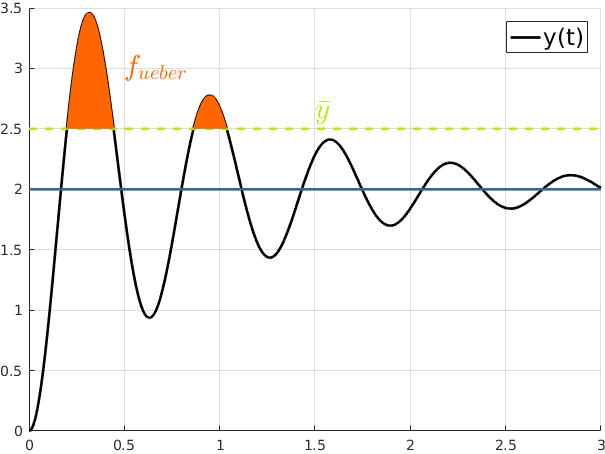
Das Schwellwertkriterium ergibt sich aus der positiven Fläche zwischen dem Systemausgang y(t) und dem Schwellwert ȳ:
Anders als beim Maximalwertkriterium fließt hier mit der Fläche sowohl die Höhe als auch der Zeitraum der Über- bzw. Unterschreitung in die Zielgröße ein. Das Schwellwertkriterium wird in Abbildung 2.2 zur Beurteilung des Überschwingers einer Sprungantwort genutzt.
Hier geht es weiter mit typischen Zielfunktionen der optimalen Regelung.
| Einleitung |
| Fehlerintegrale und zeitgewichtete Fehlerintegrale |
| Punkt- und abschnittsweise bewertende Kriterien |
| Optimale Regelung |
| Modellprädiktive Regelung |
| Referenzen |