Poker und Black Jack
Samstag, 17. Mai 2008, ab 14 Uhr
Was ist eine Gewinnstrategie beim Black Jack (der Casino-Variante von "17 und 4")? Wie kann man mit Hilfe der Mathematik des Zufalls (Wahrscheinlichkeitstheorie) seine Chancen beim Poker vergrößern? Welche Anwendungen gibt es darüber hinaus noch? Solche Fragen werden an diesem Nachmittag untersucht. Um das erworbene Wissen anzuwenden (oder einfach nur Spaß zu haben), endet der Tag mit einem Pokerturnier, bei dem es interessante Preise zu gewinnen gibt.
Computertomographie und Mathematik
29./30. August 2008
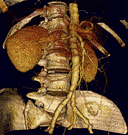
Phantom-Tumor oder Krankheit? Bilder der inneren Organe zu erstellen, ohne in den Körper einzudringen, ist eine große Errungenschaft der Medizin. Eines der wichtigsten bildgebenden Verfahren ist die Computertomographie. Hinter dieser Technik steckt - nach außen hin unsichtbar - ein hohes Maß an mathematischem Know-how. Der Schülertag Computertomographie sieht einen Besuch im CT-Zentrum des Brüderkrankenhauses Paderborn vor und einen Tag in der Uni Paderborn zum Kennenlernen und Ausprobieren der mathematischen Methoden, spielerisch und mit viel Freude, auch am abschließenden Wettbewerb.
Virusdynamik
6. - 8. Oktober 2008 und alternativ 10. - 12. Dezember 2008
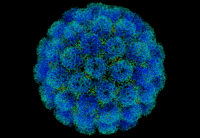
Mathematik und Biologie? Wie das zusammenpasst, erfährst du in diesem Workshop! Entwickle mit uns ein Modell, das die Ausbreitung eines Virus simuliert. Lerne in Kleingruppen Arbeitsweisen und Lösungsansätze der modernen Mathematik mit Hilfe von Computern kennen.
Bildanalyse und Bildkompression
12. - 14. November 2008
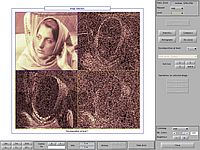
Ein Bild im Computer ist eine Masse aus Pixeln, die deine Festplatte locker im Griff hat? Lerne, dass hinter diesen Daten mehr steckt als nur Pixel und erlange einen Einblick in die Welt der Bildanalyse. In diesem Workshop wollen wir dir eine Einführung in ein modernes Stück Mathematik und eines seiner vielfältigen Anwendungsgebiete wie die JPEG2000-Bild-Kompression geben.
Billardgeometrie
Donnerstag, 20. November 2008
Welche Bahnen kann eine Billardkugel durchlaufen? Gibt es geschlossene Bahnen mit vorgegebener Anzahl von Bandenberührungen? Kann die Kugel so angestoßen werden, dass sie alle Punkte des Tisches erreicht? Was passiert, wenn man statt eines Rechteckes auch andere Tischgeometrien zulässt? Solche und andere Fragen sollen mathematisch und in Simulationen untersucht werden.