Forschungsschwerpunkte

T. Berger, C. M. Hackl and S. Trenn
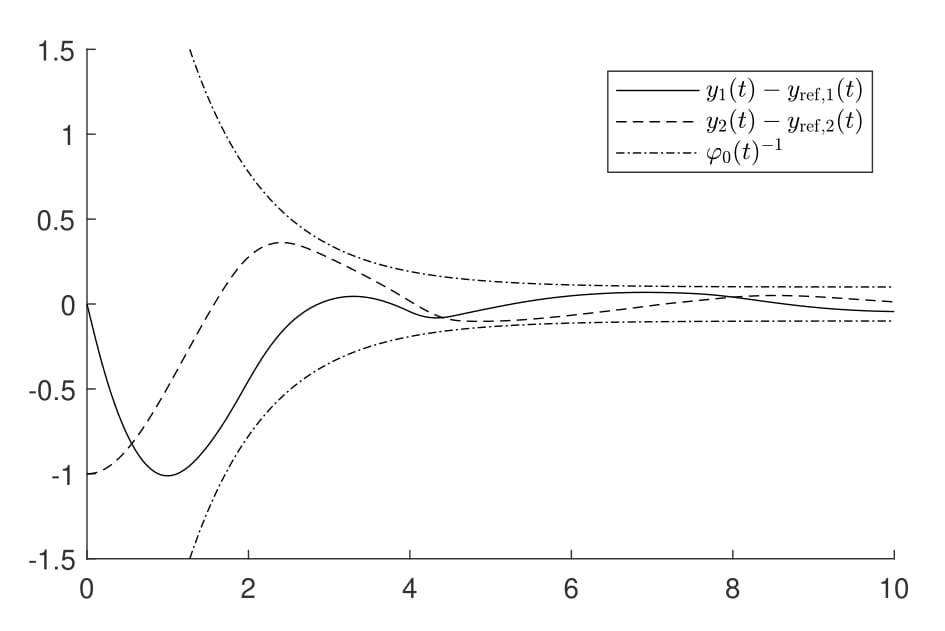
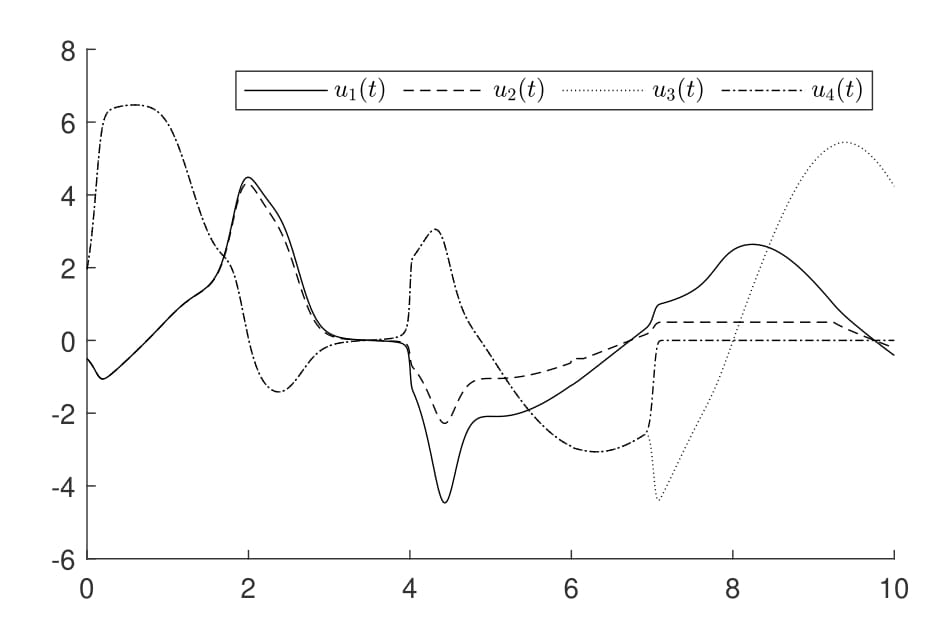
Asymptotic tracking by funnel control with internal models
to appear in: Proceedings of the European Control Conference 2024 [preprint]

T. Berger und L. Lanza
Funnel control of linear systems with arbitrary relative degree under output measurement losses
IMA Journal of Mathematical Control and Information 40 (4), 691-713, 2023 [preprint]
doi: 10.1093/imamci/dnad029

T. Berger
Fault tolerant funnel control for uncertain linear systems
IEEE Transactions on Automatic Control 66 (9), 4349-4356, 2021 [preprint]
doi: 10.1109/TAC.2020.3030759

T. Berger
Tracking with prescribed performance for linear non-minimum phase systems
Automatica 115, Article 108909, 2020 [preprint]
doi: 10.1016/j.automatica.2020.108909

T. Berger und T. Reis
Funnel control via funnel pre-compensator for minimum phase systems with relative degree two
IEEE Transactions on Automatic Control 63 (7), 2264-2271, 2018 [preprint]
doi: 10.1109/TAC.2017.2761020

T. Berger, A. Ilchmann, E. P. Ryan
Funnel control - a survey
eingereicht bei: Annual Reviews in Control [pdf]

T. Berger
Input-constrained funnel control of nonlinear systems
IEEE Transactions on Automatic Control 69 (8), 5368-5382, 2024 [preprint]
doi: 10.1109/TAC.2024.3352362

T. Berger, A. Ilchmann, E. P. Ryan
Funnel control of nonlinear systems
Mathematics of Control, Signals, and Systems 33, 151-194, 2021 [preprint]
doi: 10.1007/s00498-021-00277-z

T. Berger, T. Reis
The Funnel Pre-Compensator
International Journal of Robust and Nonlinear Control 28 (16), 4747-4771, 2018 [preprint]
doi: 10.1002/rnc.4281

T. Berger, Le Huy Hoang, T. Reis
Funnel control for nonlinear systems with known strict relative degree
Automatica 87, 345-357, 2018 [preprint]
doi: 10.1016/j.automatica.2017.10.017

T. Berger, M. Puche, F. L. Schwenninger
Funnel control for a moving water tank
Automatica 135, Article 109999, 2022 [preprint]
doi: 10.1016/j.automatica.2021.109999

T. Berger
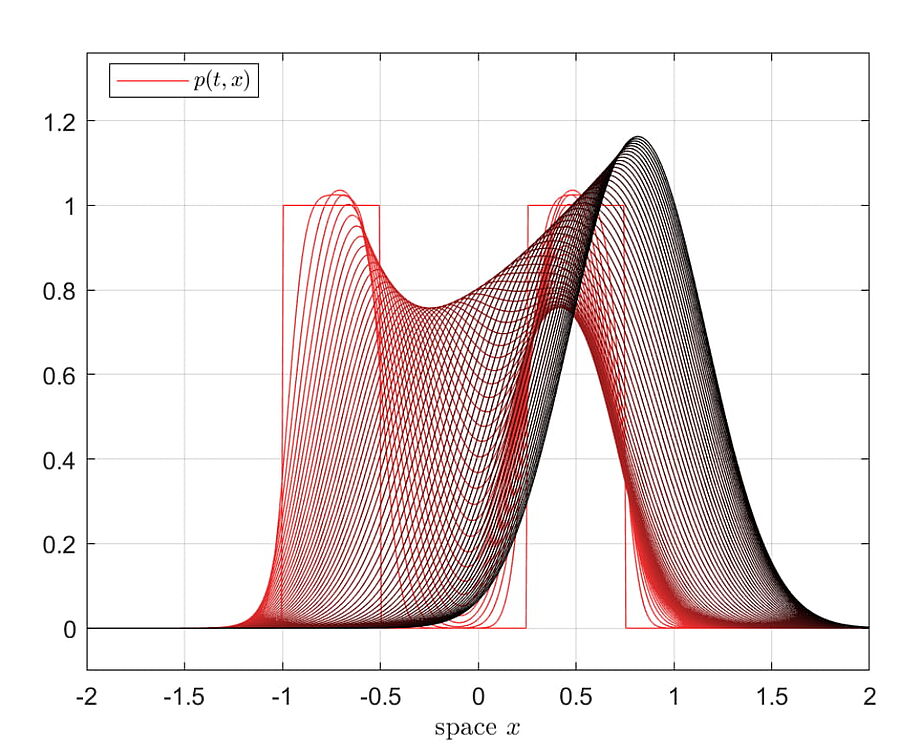
Funnel control of the Fokker-Planck equation for a multi-dimensional Ornstein-Uhlenbeck process
SIAM Journal on Control and Optimization 59 (5), 3203-3230, 2021 [preprint]
doi: 10.1137/20M1382155

T. Berger, T. Breiten, M. Puche, T. Reis
Funnel control for the monodomain equations with the FitzHugh-Nagumo model
Journal of Differential Equations 286, 164-214, 2021 [preprint]
doi: 10.1016/j.jde.2021.03.012

T. Berger, M. Puche, F. L. Schwenninger
Funnel control in the presence of infinite-dimensional internal dynamics
Systems & Control Letters 139, Article 104678, 2020 [preprint]
doi: 10.1016/j.sysconle.2020.104678

T. Berger, B. Besselink
String stability and guaranteed safety via funnel cruise control for vehicle platoons
eingereicht bei: IEEE Transactions on Automatic Control [pdf]

T. Berger, F. Nüske
Funnel control for Langevin dynamics
eingereicht bei: Automatica [pdf]

S. Drücker, L. Lanza, T. Berger, T. Reis, R. Seifried
Experimental validation for the combination of funnel control with a feedforward control strategy
Multibody System Dynamics 2024 [pdf]
doi: 10.1007/s11044-024-09976-2 (open access)

Z. Guo, X. Gu, Y. Han, J. Guo, T. Berger
Maneuvering tracking algorithm for reentry vehicles with guaranteed prescribed performance
IEEE Transactions on Aerospace and Electronic Systems 60 (3), 3012-3020, 2024 [preprint]
doi: 10.1109/TAES.2024.3357649

J. G. Lee, T. Berger, S. Trenn, H. Shim
Edge-wise funnel output synchronization of heterogeneous agents with relative degree one
Automatica 156, Article 111204, 2023 [preprint]
doi: 10.1016/j.automatica.2023.111204 (open access)

T. Berger
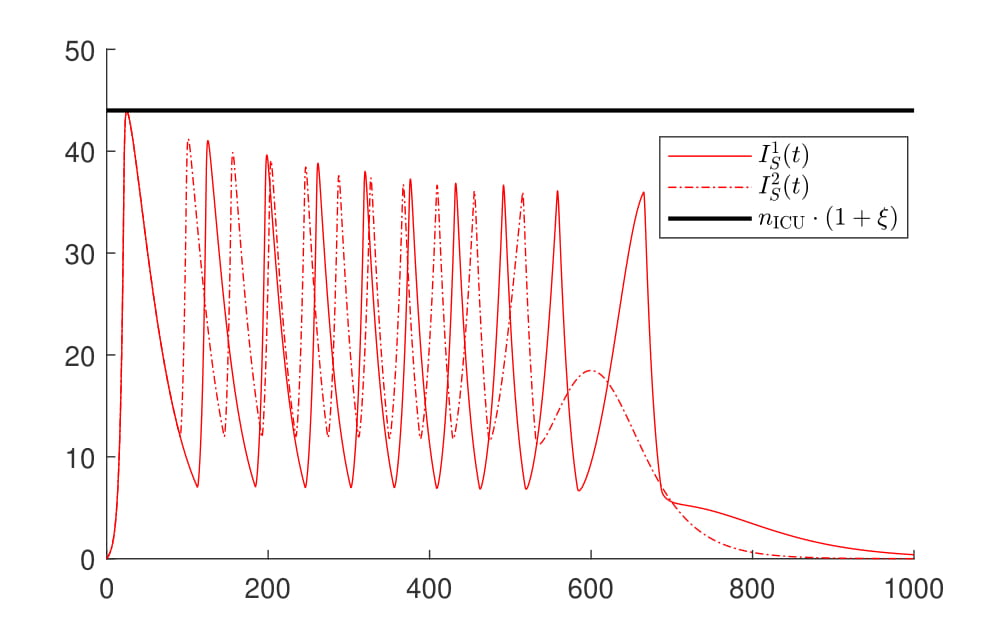
Feedback control of the COVID-19 pandemic with guaranteed non-exceeding ICU capacity
Systems & Control Letters 160, Article 105111, 2022 [preprint]
doi: 10.1016/j.sysconle.2021.105111

T. Berger, L. Lanza
Output tracking for a non-minimum phase robotic manipulator
IFAC-PapersOnLine 54 (9), 178-185, 2021 [preprint]
doi: 10.1016/j.ifacol.2021.06.074

T. Berger, S. Drücker, L. Lanza, T. Reis, R. Seifried
Tracking control for underactuated non-minimum phase multibody systems
Nonlinear Dynamics 104 (4), 3671-3699, 2021 [preprint]
doi: 10.1007/s11071-021-06458-4

T. Berger, A.-L. Rauert
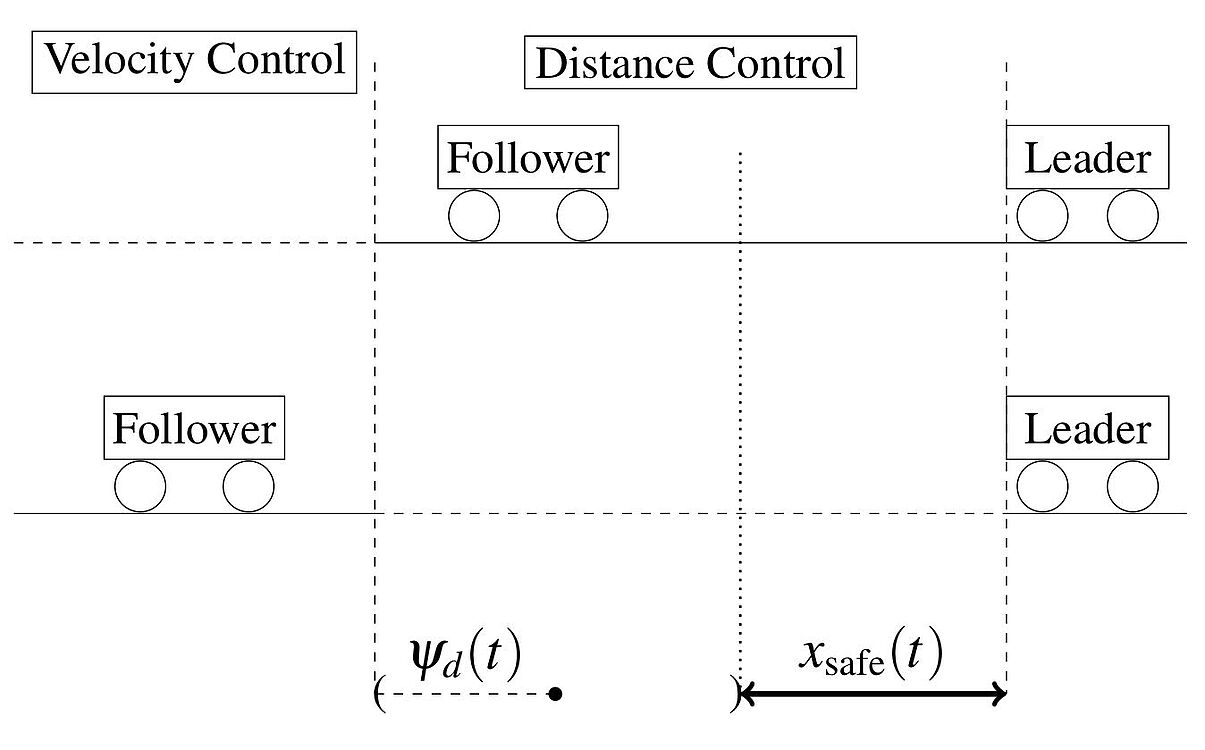
Funnel cruise control
Automatica 119, Article 109061, 2020 [preprint]
doi: 10.1016/j.automatica.2020.109061

T. Berger, S. Otto, T. Reis, R. Seifried
Combined open-loop and funnel control for underactuated multibody systems
Nonlinear Dynamics 95 (3), 1977-1998, 2019 [preprint]
doi: 10.1007/s11071-018-4672-5

L. Lanza, D. Dennstädt, T. Berger, K. Worthmann
Safe continual learning in model predictive control with prescribed bounds on the tracking error
eingereicht bei: International Journal of Robust and Nonlinear Control [pdf]

B. Oppeneiger, L. Lanza, M. Schell, D. Dennstädt, M. Schaller, B. Zamzow, T. Berger, K. Worthmann
Model predictive control of a magnetic levitation system with prescribed output tracking performance
Control Engineering Practice 151, Article 106018, 2024 
doi: 10.1016/j.conengprac.2024.106018 (open access)

T. Berger, D. Dennstädt, L. Lanza, K. Worthmann
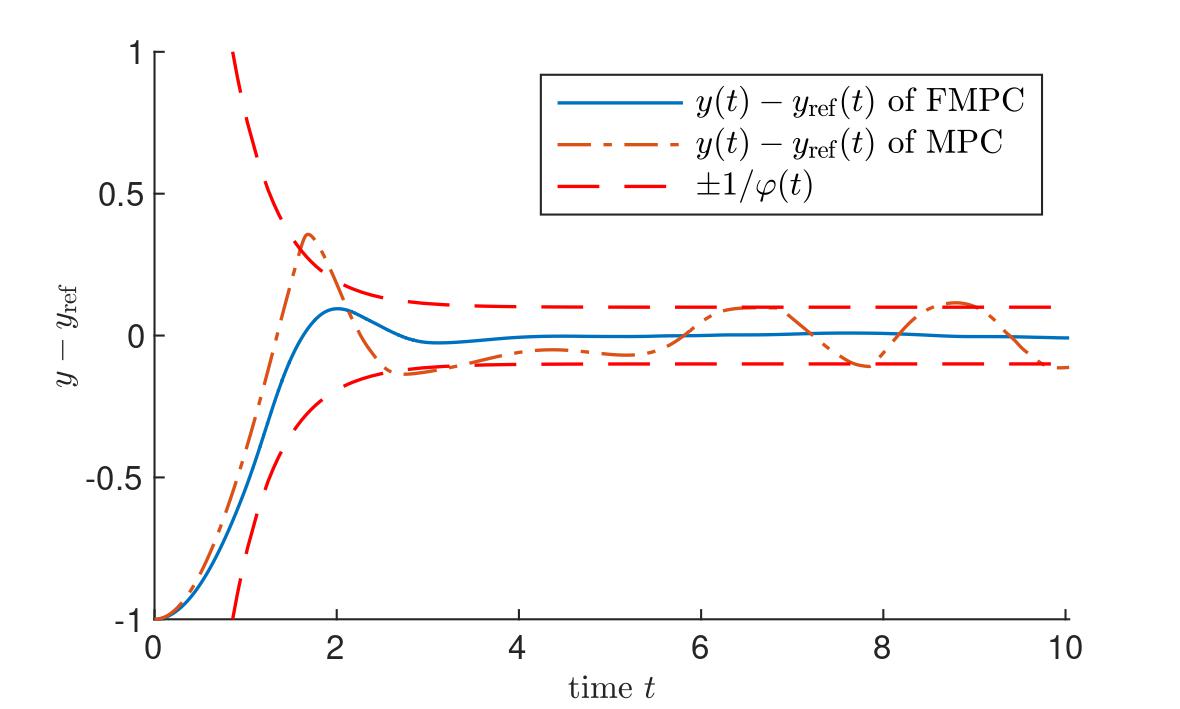
Robust Funnel Model Predictive Control for Output Tracking with Prescribed Performance
SIAM Journal on Control and Optimization 62 (4), 2071-2097, 2024 [preprint]
doi: 10.1137/23M1551195

T. Berger, D. Dennstädt
Funnel MPC for nonlinear systems with arbitrary relative degree
Automatica 167, Article 111759, 2024 [preprint]
doi: 10.1016/j.automatica.2024.111759 (open access)

T. Berger, D. Dennstädt, A. Ilchmann, K. Worthmann
Funnel MPC for nonlinear systems with relative degree one
SIAM Journal on Control and Optimization 60 (6), 3358-3383, 2022 [preprint]
doi: 10.1137/21M1431655

T. Berger, D. Dennstädt
Funnel MPC with feasibility constraints for nonlinear systems with arbitrary relative degree
IEEE Control Systems Letters 6, 2804-2809, 2022 [preprint]
doi: 10.1109/LCSYS.2022.3178478

T. Berger, C. Kästner, K. Worthmann
Learning-based Funnel-MPC for output-constrained nonlinear systems
IFAC-PapersOnLine 53 (2), 5177-5182, 2020 [preprint]
doi: 10.1016/j.ifacol.2020.12.1186

T. Berger, T. Reis, S. Trenn
Observability of linear differential-algebraic systems - a survey
In: Achim Ilchmann and Timo Reis (eds.) Surveys in Differential-Algebraic Equations IV, Differential-Algebraic Equations Forum, pp. 161-219. Springer, Berlin-Heidelberg, 2017 [preprint]
doi: 10.1007/978-3-319-46618-7_4

T. Berger, T. Reis
Controllability of linear differential-algebraic systems - a survey
In: Achim Ilchmann and Timo Reis (eds.) Surveys in Differential-Algebraic Equations I, Differential-Algebraic Equations Forum, pp. 1-61. Springer, Berlin-Heidelberg, 2013 [preprint]
doi: 10.1007/978-3-642-34928-7_1

T. Berger, A. Ilchmann, S. Trenn
Quasi feedback forms for differential-algebraic systems
IMA Journal of Mathematical Control and Information 39 (2), 533-563, 2022 [preprint]
doi: 10.1093/imamci/dnab030

T. Berger
The zero dynamics form for nonlinear differential-algebraic systems
IEEE Transactions on Automatic Control 62 (8), 4131-4137, 2017 [preprint]
doi: 10.1109/TAC.2016.2620561

T. Berger
Zero dynamics and funnel control of general linear differential-algebraic systems
ESAIM: Control, Optimisation and Calculus of Variations 22 (2), 371-403, 2016 [preprint]
doi: 10.1051/cocv/2015010

T. Berger, C. Trunk, H. Winkler
Linear relations and the Kronecker canonical form
Linear Algebra and its Applications 488, 13-44, 2016 [preprint]
doi: 10.1016/j.laa.2015.09.033

T. Berger, P. Van Dooren
Computing the regularization of a linear differential-algebraic system
Systems & Control Letters 86, 48-53, 2015 [preprint]
doi: 10.1016/j.sysconle.2015.10.003

T. Berger, S. Trenn
Kalman controllability decompositions for differential-algebraic systems
Systems & Control Letters 71, 54-61, 2014 [preprint]
doi: 10.1016/j.sysconle.2014.06.004

T. Berger, S. Trenn
Addition to "The quasi-Kronecker form for matrix pencils"
SIAM Journal on Matrix Analysis and Applications 34 (1), 94–101, 2013 [pdf]
doi: 10.1137/120883244

T. Berger, A. Ilchmann
On the standard canonical form of time-varying linear DAEs
Quarterly of Applied Mathematics 71 (1), 69-87, 2013 [preprint]
doi: 10.1090/S0033-569X-2012-01285-1

T. Berger, A. Ilchmann, T. Reis
Normal forms, high-gain and funnel control for linear differential-algebraic systems
In: L.T. Biegler, S.L. Campbell, V. Mehrmann (eds.) Control and Optimization with Differential-Algebraic Constraints, Advances in Design and Control, vol. 23, pp. 127–164. SIAM, Philadelphia, 2012 [preprint]
doi: 10.1137/9781611972252.ch7

T. Berger, S. Trenn
The quasi-Kronecker form for matrix pencils
SIAM Journal on Matrix Analysis and Applications 33 (2), 336-368, 2012 [pdf]
doi: 10.1137/110826278

T. Berger, A. Ilchmann, T. Reis
Zero dynamics and funnel control of linear differential-algebraic systems
Mathematics of Control, Signals and Systems 24 (3), 219-263, 2012 [preprint]
doi: 10.1007/s00498-012-0085-z

T. Berger, A. Ilchmann, S. Trenn
The quasi-Weierstraß form for regular matrix pencils
Linear Algebra and its Applications 436 (10), 4052-4069, 2012 [preprint]
doi: 10.1016/j.laa.2009.12.036

T. Berger, H. Gernandt, C. Trunk, H. Winkler, M. Wojtylak
The gap distance to the set of singular matrix pencils
Linear Algebra and its Applications 564, 28-57, 2019 [preprint]
doi: 10.1016/j.laa.2018.11.020

T. Berger, A. Ilchmann, F. Wirth
Zero dynamics and stabilization for analytic linear systems
Acta Applicandae Mathematicae 138 (1), 17-57, 2015 [preprint]
doi: 10.1007/s10440-014-9956-2

T. Berger
Zero dynamics and stabilization for linear DAEs
In: Sebastian Schöps, Andreas Bartel, Michael Günther, E. Jan W. ter Maten, and Peter C. Müller (eds.) Progress in Differential-Algebraic Equations, Differential-Algebraic Equations Forum, pp. 21-45. Springer, Berlin-Heidelberg, 2014 [preprint]
doi: 10.1007/978-3-662-44926-4_2

T. Berger
Robustness of stability of time-varying index-1 DAEs
Mathematics of Control, Signals, and Systems 26 (3), 403-433, 2014 [preprint]
a more comprehensive preprint version can be found here: [preprint2]
doi: 10.1007/s00498-013-0123-5

T. Berger, A. Ilchmann
On stability of time-varying linear differential-algebraic equations
International Journal of Control 86 (6), 1060-1076, 2013 [preprint]
doi: 10.1080/00207179.2013.773087

T. Berger
Bohl exponent for time-varying linear differential-algebraic equations
International Journal of Control 85 (10), 1433-1451, 2012 [preprint]
doi: 10.1080/00207179.2012.688872

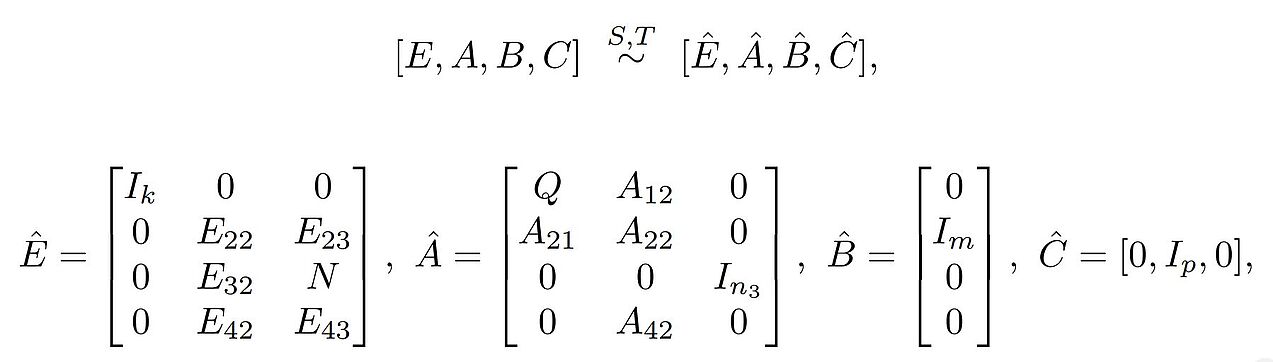
T. Berger, Le Huy Hoang, T. Reis
Vector relative degree and funnel control for differential-algebraic systems
In: Sara Grundel, Timo Reis, and Sebastian Schöps (eds.) Progress in Differential-Algebraic Equations II, Differential-Algebraic Equations Forum, pp. 213-255. Springer, Cham, 2020 [preprint]
doi: 10.1007/978-3-030-53905-4_8

T. Berger
Zero dynamics and funnel control of general linear differential-algebraic systems
ESAIM: Control, Optimisation and Calculus of Variations 22 (2), 371-403, 2016 [preprint]
doi: 10.1051/cocv/2015010

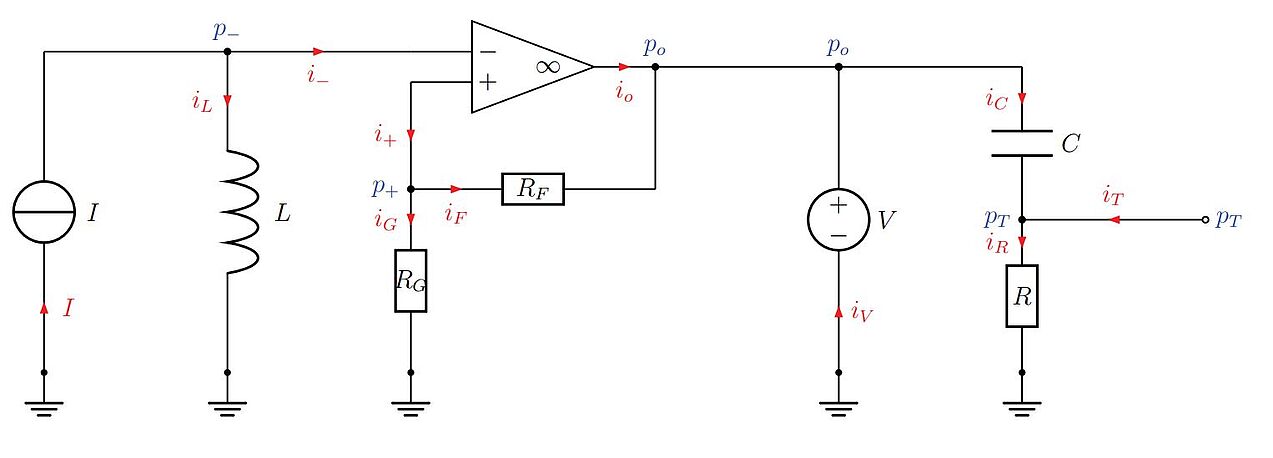
T. Berger, T. Reis
Zero dynamics and funnel control for linear electrical circuits
Journal of the Franklin Institute 351 (11), 5099–5132, 2014 [preprint]
doi: 10.1016/j.jfranklin.2014.08.006

T. Berger, A. Ilchmann, T. Reis
Normal forms, high-gain and funnel control for linear differential-algebraic systems
In: L.T. Biegler, S.L. Campbell, V. Mehrmann (eds.) Control and Optimization with Differential-Algebraic Constraints, Advances in Design and Control, vol. 23, pp. 127–164. SIAM, Philadelphia, 2012 [preprint]
doi: 10.1137/9781611972252.ch7

T. Berger, A. Ilchmann, T. Reis
Zero dynamics and funnel control of linear differential-algebraic systems
Mathematics of Control, Signals and Systems 24 (3), 219-263, 2012 [preprint]
doi: 10.1007/s00498-012-0085-z

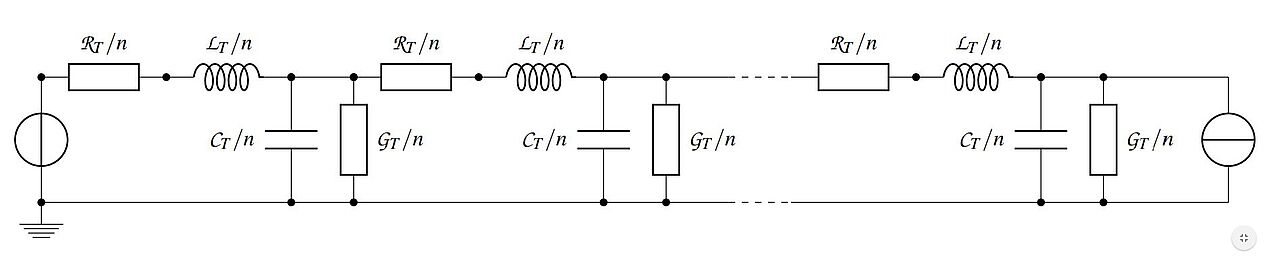
T. Berger, A. Ilchmann and T. Reis
Funnel control for nonlinear functional differential-algebraic systems
Proceedings of the MTNS 2014, Groningen, The Netherlands, pp. 46-53, 2014 [pdf]

J. Jaiswal, T. Berger, N. K. Tomar
Partial causal detectability of linear descriptor systems and existence of functional ODE estimators
eingereicht bei: SIAM Journal on Control and Optimization [pdf]

J. Jaiswal, T. Berger, N. K. Tomar
Partial detectability and generalized functional observer design for linear descriptor systems
eingereicht bei: Franklin Open [pdf]

J. Jaiswal, T. Berger, N. K. Tomar
Existence conditions for functional ODE observer design of descriptor systems revisited
Journal of the Franklin Institute 361 (8), Article 106848, 2024 [preprint]
doi: 10.1016/j.jfranklin.2024.106848

J. Jaiswal, T. Berger, N. K. Tomar
Partial impulse observability of linear descriptor systems
Systems & Control Letters 168, Article 105352, 2022 [preprint]
doi: 10.1016/j.sysconle.2022.105352

T. Berger, L. Lanza
Observers for differential-algebraic systems with Lipschitz or monotone nonlinearities
In: Sara Grundel, Timo Reis, and Sebastian Schöps (eds.) Progress in Differential-Algebraic Equations II, Differential-Algebraic Equations Forum, pp. 257-289. Springer, Cham, 2020 [preprint]
doi: 10.1007/978-3-030-53905-4_9

T. Berger, T. Reis
ODE observers for DAE systems
IMA Journal of Mathematical Control and Information 36 (4), 1375-1393, 2019 [preprint]
doi: 10.1093/imamci/dny032

T. Berger
On observers for nonlinear differential-algebraic systems
IEEE Transactions on Automatic Control 64 (5), 2150-2157, 2019 [preprint]
doi: 10.1109/TAC.2018.2866438

T. Berger
Disturbance decoupled estimation for linear differential-algebraic systems
International Journal of Control 92 (3), 593-612, 2019 [preprint]
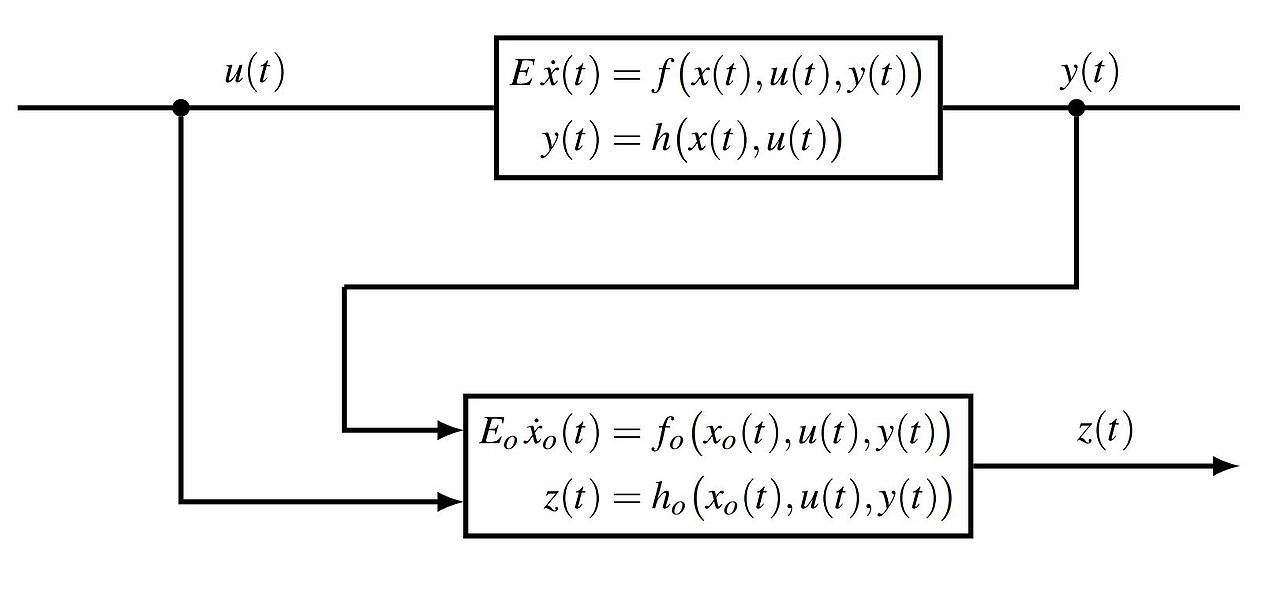
doi: 10.1080/00207179.2017.1363411

T. Berger, T. Reis
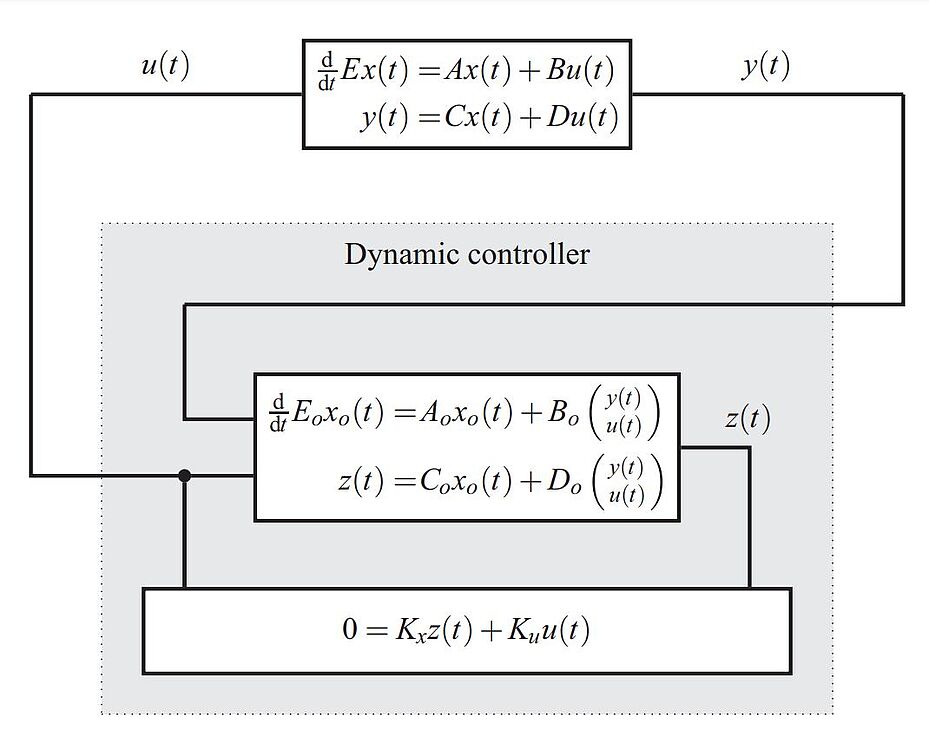
Observers and dynamic controllers for linear differential-algebraic systems
SIAM Journal on Control and Optimization 55 (6), 3564-3591, 2017 [pdf]
doi: 10.1137/15M1035355

T. Berger
Disturbance decoupling by behavioral feedback for linear differential-algebraic systems
Automatica 80, 272-283, 2017 [preprint]
doi: 10.1016/j.automatica.2017.01.012

T. Berger
Controlled invariance for nonlinear differential-algebraic systems
Automatica 64, 226-233, 2016 [preprint]
doi: 10.1016/j.automatica.2015.11.024

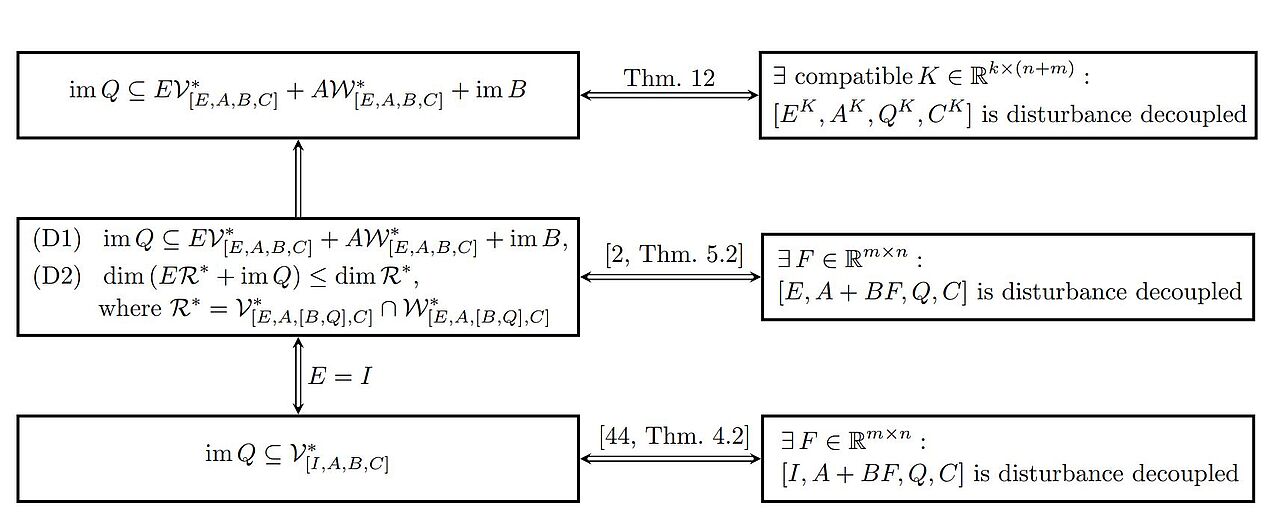
T. Berger, T. Reis
Regularization of linear time-invariant differential-algebraic systems
Systems & Control Letters 78, 40-46, 2015 [preprint]
doi: 10.1016/j.sysconle.2015.01.013

T. Berger, N. Karcanias, M. Livada
The pseudo-McMillan degree of implicit transfer functions of RLC networks
Circuits, Systems, and Signal Processing 38 (3), 967-985, 2019 [preprint]
doi: 10.1007/s00034-018-0921-6

T. Berger, G. Halikias, N. Karcanias
Effects of dynamic and non-dynamic element changes in RC and RL networks
International Journal of Circuit Theory and Applications 43 (1), 36-59, 2015 [preprint]
doi: 10.1002/cta.1923

T. Berger, T. Reis
Zero dynamics and funnel control for linear electrical circuits
Journal of the Franklin Institute 351 (11), 5099-5132, 2014 [preprint]
doi: 10.1016/j.jfranklin.2014.08.006

T. Berger, T. Reis
Structural properties of positive real and reciprocal rational matrices
Proceedings of the MTNS 2014, Groningen, The Netherlands, pp. 402-409, 2014 [pdf]